在东西方向的海岸线,上有一长为1km的码头MN(如图,MN=lkm),在码头西端M的正西19.5 km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西3000,且与A相距40km的B处;经过l小时20分钟,又测得该轮船位于A的北偏东6000方向,且与A相距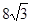 km的C处.
km的C处.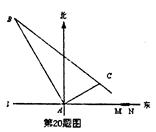
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
如图①,②,在平面直角坐标系 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点 为圆心,4为半径的圆与
为圆心,4为半径的圆与 轴交于
轴交于 ,
, 两点,
两点, 为弦,
为弦, ,
, 是
是 轴上的一动点,连结
轴上的一动点,连结 。
。
(1)求 的度数;
的度数;
(2)如图①,当 与⊙A相切时,求
与⊙A相切时,求 的长;
的长;
(3)如图②,当点 在直径
在直径 上时,
上时, 的延长线与⊙A相交于点
的延长线与⊙A相交于点 ,问
,问 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG。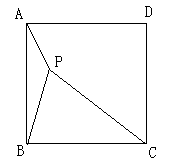
(1)△ABP以点B为旋转中心旋转了度;
(2)求出PG的长度;(3)以点G为圆心,r为半径作⊙G:
①当半径r满足时,⊙G与边PC只有一个交点;
②当半径r满足时,⊙G与边PC有两个交点;
③当半径r满足时,⊙G与边PC没有交点。
永定土楼是世界文化遗产“福建土楼”的组成部分,是闽西的旅游胜地. “永定土楼”模型深受游客喜爱.其中某种规格土楼模型的单价y(元)与购买数量x(个)之间的函数关系如下:当0<x≤10时,y=200;当10<x<20时,y=-5x+250;当x≥20时,y=150。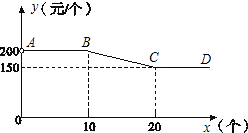
(1)若甲旅游团购买该种规格的土楼模型10个,则一共需要 元;若乙旅游团购买该种规格的土楼模型20个,则一共需要 元。
(2)某旅游团购买该种规格的土楼模型总金额为2625元,问该旅游团共购买这种土楼模型多少个?(总金额=数量×单价)
如图,有两个边长为2的正方形,将其中一个正方形沿对角线剪开成两个全等的等腰直角三角形,用这三个图片分别在网格备用图的基础上(只要再补出两个等腰直角三角形即可),分别拼符合要求的图形:(如图1)


图1图2
既不是轴对称图形,又不是中心对称图形是轴对称图形,不是中心对称图形

图3图4
是中心对称图形,不是轴对称图形既是轴对称图形,又是中心对称图形
如图,AE是圆O的直径,点B在AE的延长线上,点D在圆O上,且AC⊥DC, AD平分∠EAC
(1)求证:BC是圆O的切线。
(2)若BE=8,BD=12,求圆O的半径,