永定土楼是世界文化遗产“福建土楼”的组成部分，是闽西的旅游胜地. “永定土楼”模型深受游客喜爱.其中某种规格土楼模型的单价y（元）与购买数量x（个）之间的函数关系如下：当0<x≤10时，y=200；当10<x<20时，y=-5x+250；当x≥20时，y=150。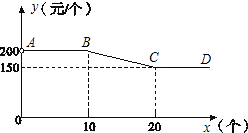
（1）若甲旅游团购买该种规格的土楼模型10个，则一共需要 元；若乙旅游团购买该种规格的土楼模型20个，则一共需要 元。
（2）某旅游团购买该种规格的土楼模型总金额为2625元，问该旅游团共购买这种土楼模型多少个？(总金额=数量×单价)
，其中
＝-2 .
（2）
，
，请回答下列回题：
；
、
互为倒数，
、
互为相反数，求（3
的值