如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG。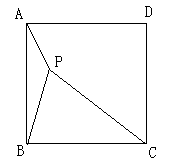
(1)△ABP以点B为旋转中心旋转了 度;
(2)求出PG的长度;(3)以点G为圆心,r为半径作⊙G:
①当半径r满足 时,⊙G与边PC只有一个交点;
②当半径r满足 时,⊙G与边PC有两个交点;
③当半径r满足 时,⊙G与边PC没有交点。
某城市按以下规定收取每月煤气费,用煤气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费.如甲用户某月份用煤气80立方米,那么这个月甲用户应交煤气费用为 元.
(1)设甲用户某月用煤气x立方米,用含x的代数式表示甲用户该月的煤气费.
若x≤60,则费用表示为 元;若x>60,则费用表示为 元.
(2)若甲用户10月份的煤气费是84元,求甲用户10月份用去煤气多少立方米?
有两根同样长度但粗细不同的蜡烛,粗烛可燃4h,细烛可燃3h,一次停电,同时点燃两根蜡烛,来电后同时吹灭,发现粗烛的长度是细烛的2倍.求停电的时间.
一个邮递员骑自行车在规定时间内把特快专递送到单位.他每小时行15千米,可以早到24分钟,如果每小时行12千米,就要迟到15分钟.原定的时间是多少?他去的单位有多远?
如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的左视图和俯视图;(用阴影表示)
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?
小明做作业时,不小心将方程中 ●的一个常数污染了看不清楚,怎么办呢?
●的一个常数污染了看不清楚,怎么办呢?
(1)小红告诉他该方程的解是x=3.那么这个常数应是多少呢?
(2)小芳告诉他该方程的解是负数,并且这个常数是负整数,请你试求该方程的解.(友情提醒:设这个常数为m.)