某饰品店老板去批发市场购买新款手链,第一次购手链共用100元,回来后该手链按定价2.8元销售,并很快售完.由于该手链深得“潮女”喜爱十分畅销,第二次去购手链时,每条的批发价已比第一次高0.5元,共用去了150元,所购数量比第一次多10条.当这批手链售出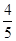 时,出现滞销,便以定价的5折售完剩余手链.(手链销售中不考虑其它因素)
时,出现滞销,便以定价的5折售完剩余手链.(手链销售中不考虑其它因素)
(1)求第一次该手链的批发价;
(2)试问该老板第二次销售手链是赔钱了,还是赚钱了?用数据说明.
为了调动同学们的学习积极性,某班班主任陈老师在班级管理中采用了奖励机制,每次期中期末考试后都会进行表彰奖励.期中考试后,陈老师花了300元购买甲、乙两种奖品用于奖励进步显著学生及成绩特别优秀学生.期末考试后,陈老师再次去购买奖品时,发现甲奖品每件上涨了6元,乙奖品每件上涨了12元,结果购买相同数量的甲、乙两种奖品却多花了120元.设陈老师每次购买甲奖品x件,乙奖品y件.
(1)请直接写出y与x之间的函数关系式: .
(2)若x=8,且这两种奖品不再调价.若陈老师再次去购买奖品,且所买甲奖品比前两次都少1件,则他最多买几件乙奖品,才能把奖品总费用控制在300元以内?
【备注:已知陈老师第一次购买奖品发现,甲奖品比乙奖品便宜,两种奖品单价(元)都在30以内且为偶数.】
如图,海岛B位于港口A的西南方向,19∶00时,甲船从港口A出发,以18海里/小时的速度先沿正西方向航行1小时到达港口C装载物资,半小时后再转向南偏西30°方向开往海岛B,结果22∶30到达.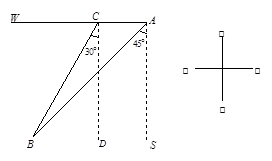
(1)求甲船从港口C驶向海岛B的速度(精确到0.1海里/小时).
(2)在甲船从港口A出发的同时,乙船也 从港口A出发以18海里/小时的速度直接开往海岛B.已知海岛B处有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船在航行途中哪一艘船先看到灯塔?
如图,AB切⊙O于点B,AC交⊙O于点M 、N,若四边形OABN恰为平行四边形,且弦BN的长为10cm.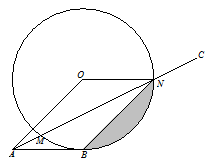
(1)求⊙O的半径长及图中阴影部分的面积S.
(2)求MN的长.
现有4根小木棒,长度分别为:2、3、3、5(单位:cm),从中任意取出3根,请用画树状图法求它们能首尾顺次相接搭成三角形的概率.
母亲节快到了,某校调查了部分学生是否知道母亲的生日情况,下面图①,图②是相应的扇形和条形统计图: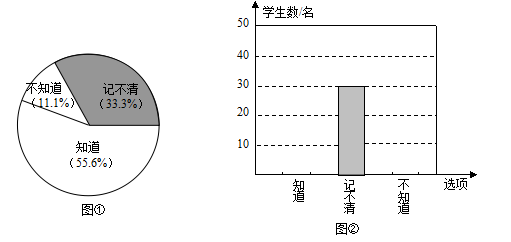
根据上图信息,解答下列问题:
(1)本次被调查学生的人数为 ,并请补全条形统计图.
(2)若全校共有2700名学生,你估计这所学校约有 名学生知道母亲的生日.
(3)通过对以上数据的分析,你有何感想?(用一句话回答)