分解因式: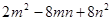
在 中, , ,点 是 上一点,连接 ,过点 作 ,在 上取点 ,连接 .延长 至 ,使 ,连接 , ,且 .
(1)若 ,求 的长;
(2)如图1,当点 在 上时,求证: ;
(3)如图2,当点 在 的垂直平分线上时,直接写出 的值.

我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数 为"吉祥数",求所有"吉祥数"中 的最大值.
近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了 .某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调 出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了 ,且储备猪肉的销量占总销量的 ,两种猪肉销售的总金额比5月20日提高了 ,求 的值.
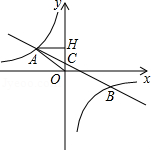
在平面直角坐标系中,一次函数 的图形与反比例函数 的图象交于第二、四象限内的 、 两点,与 轴交于 点,过点 作 轴,垂足为 , , ,点 的坐标为 .
(1)求 的周长;
(2)求该反比例函数和一次函数的解析式.
为响应"全民阅读"号召,某校在七年级800名学生中随机抽取100名学生,对该年级学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的 ,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.
