我们知道，任意一个正整数n都可以进行这样的分解：np×q(p-优题课

题文

我们知道，任意一个正整数 $n$ 都可以进行这样的分解： $n = p \times q (p$ ， $q$ 是正整数，且 $p ⩽ q)$ ，在 $n$ 的所有这种分解中，如果 $p$ ， $q$ 两因数之差的绝对值最小，我们就称 $p \times q$ 是 $n$ 的最佳分解．并规定： $F (n) = \frac{p}{q}$ ．例如12可以分解成 $1 \times 12$ ， $2 \times 6$ 或 $3 \times 4$ ，因为 $12 - 1 > 6 - 2 > 4 - 3$ ，所以 $3 \times 4$ 是12的最佳分解，所以 $F (12) = \frac{3}{4}$ ．

（1）如果一个正整数 $a$ 是另外一个正整数 $b$ 的平方，我们称正整数 $a$ 是完全平方数．求证：对任意一个完全平方数 $m$ ，总有 $F (m) = 1$ ；

（2）如果一个两位正整数 $t$ ， $t = 10 x + y (1 ⩽ x ⩽ y ⩽ 9$ ， $x$ ， $y$ 为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数 $t$ 为"吉祥数"，求所有"吉祥数"中 $F (t)$ 的最大值．

科目数学题型解答题难度中等

知识点：列代数式有理数的混合运算

登录免费查看答案和解析

相关试题

已知关于 $x$ 的方程 $x^{2} - 4 x + k + 1 = 0$ 有两实数根．

（1）求 $k$ 的取值范围；

（2）设方程两实数根分别为 $x_{1}$ 、 $x_{2}$ ，且 $\frac{3}{x_{1}} + \frac{3}{x_{2}} = x_{1} x_{2} - 4$ ，求实数 $k$ 的值．

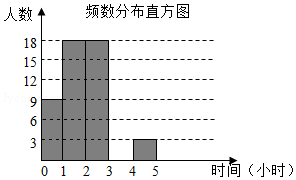
某校为了了解全校学生线上学习情况，随机选取该校部分学生，调查学生居家学习时每天学习时间（包括线上听课及完成作业时间）．如图是根据调查结果绘制的统计图表．请你根据图表中的信息完成下列问题：

频数分布表

学习时间分组	频数	频率
$A$ 组 $(0 ⩽ x < 1)$	9	$m$
$B$ 组 $(1 ⩽ x < 2)$	18	0.3
$C$ 组 $(2 ⩽ x < 3)$	18	0.3
$D$ 组 $(3 ⩽ x < 4)$	$n$	0.2
$E$ 组 $(4 ⩽ x < 5)$	3	0.05

（1）频数分布表中 $m =$ 　　， $n =$ 　　，并将频数分布直方图补充完整；

（2）若该校有学生1000名，现要对每天学习时间低于2小时的学生进行提醒，根据调查结果，估计全校需要提醒的学生有多少名？

（3）已知调查的 $E$ 组学生中有2名男生1名女生，老师随机从中选取2名学生进一步了解学生居家学习情况．请用树状图或列表求所选2名学生恰为一男生一女生的概率．

如图，在平行四边形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 交于点 $O$ ，点 $M$ ， $N$ 分别为 $OA$ 、 $OC$ 的中点，延长 $BM$ 至点 $E$ ，使 $EM = BM$ ，连接 $DE$ ．

（1）求证： $ΔAMB ≅ ΔCND$ ；

（2）若 $BD = 2 AB$ ，且 $AB = 5$ ， $DN = 4$ ，求四边形 $DEMN$ 的面积．

先化简 $\frac{x^{2} - 4 x + 4}{x^{2} - 1} \div \frac{x^{2} - 2 x}{x + 1} + \frac{1}{x - 1}$ ，再从 $- 2$ ． $- 1$ ，0，1，2中选一个合适的数作为 $x$ 的值代入求值．

如图，抛物线 $y = a x^{2} + \frac{9}{4} x + c$ 经过点 $A (- 1, 0)$ 和点 $C (0, 3)$ 与 $x$ 轴的另一交点为点 $B$ ，点 $M$ 是直线 $BC$ 上一动点，过点 $M$ 作 $MP / / y$ 轴，交抛物线于点 $P$ ．

（1）求该抛物线的解析式；

（2）在抛物线上是否存在一点 $Q$ ，使得 $ΔQCO$ 是等边三角形？若存在，求出点 $Q$ 的坐标；若不存在，请说明理由；

（3）以 $M$ 为圆心， $MP$ 为半径作 $⊙ M$ ，当 $⊙ M$ 与坐标轴相切时，求出 $⊙ M$ 的半径．

试卷网试题网古诗词网作文网范文网