设实数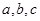 成等比数列,非零实数
成等比数列,非零实数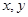 分别为
分别为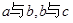 的等差中项,求证
的等差中项,求证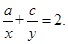
在复平面上,平行四边形ABCD的三个顶点A、B、C 对应的复数分别为 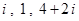 . 求第四个顶点D的坐标及此平行四边形的对角线的长.
. 求第四个顶点D的坐标及此平行四边形的对角线的长.
某机构为了研究人的脚的大小与身高之间的关系,随机测量了20人,得到如下数据
| 身高(厘米) |
192 |
164 |
172 |
177 |
176 |
159 |
171 |
166 |
182 |
166 |
| 脚长(码) |
48 |
38 |
40 |
43 |
44 |
37 |
40 |
39 |
46 |
39 |
| 身高(厘米) |
169 |
178 |
167 |
174 |
168 |
179 |
165 |
170 |
162 |
170 |
| 脚长(码) |
43 |
41 |
40 |
43 |
40 |
44 |
38 |
42 |
39 |
41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,请根据上表数据完成下面的2×2列联表。
| 高个 |
非高个 |
合计 |
|
| 大脚 |
|||
| 非大脚 |
12 |
||
| 合计 |
20 |
(2)根据(1)中的2×2列联表,若按99%可靠性要求,能否认为脚的大小与身高之间有关系。
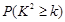 |
0.050 0.010 0.001 |
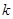 |
3.841 6.635 10.828 |
参考公式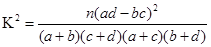
已知实数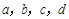 满足
满足 ,
,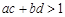 ,求证
,求证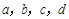 中至少有一个是负数.
中至少有一个是负数.
设m∈R,复数z=2m2-3m-2+(m2-3m+2)i.试求m为何值时,z分别为:
(1)实数;(2)虚数;(3)纯虚数