(本小题满分12分)
椭圆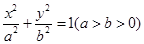 的一个焦点
的一个焦点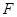 与抛物线
与抛物线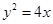 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为
,倾斜角为 的直线
的直线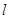 过点
过点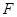 .
.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为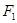 ,问抛物线
,问抛物线 上是否存在一点
上是否存在一点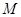 ,使得
,使得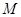 与
与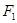 关于直线
关于直线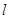 对称,若存在,求出点
对称,若存在,求出点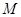 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本小题满分12分)如图,已知底角为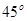 的等腰梯形
的等腰梯形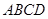 ,底边
,底边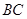 长为7
长为7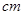 ,腰长为
,腰长为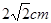 ,当一条垂直于底边
,当一条垂直于底边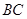
(垂足为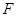 )的直线
)的直线 从左至右移动(与梯形
从左至右移动(与梯形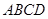 有公共点)时,直线
有公共点)时,直线 把梯形分成两部分,令
把梯形分成两部分,令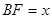 ,
,
(1)试写出直线 左边部分的面积
左边部分的面积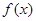 与
与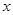 的函数.
的函数.
(2)已知 ,
,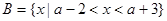 ,若
,若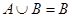 ,求
,求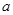 的取值范围.
的取值范围.
(本小题满分12分)已知命题 是增函数,命题
是增函数,命题 关于
关于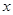 的不等式
的不等式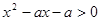 恒成立;若
恒成立;若 为真,
为真,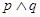 为假,求
为假,求 的取值范围.
的取值范围.
(本小题满分12分)
(1)写出命题“若 ,则
,则 ”的逆命题、否命题及逆否命题;
”的逆命题、否命题及逆否命题;
(2)写出命题“ ”的否定形式.
”的否定形式.
(本小题满分10分)已知全集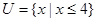 ,集合
,集合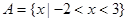 ,集合
,集合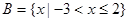 ,
,
求: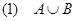 ;
;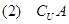 ;
;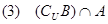 .
.
(本小题满分12分) 已知中心为坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点;
(1)求椭圆C的标准方程;
(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在求出直线方程;若不存在说明理由。