某学校为了了解学生的日平均睡眠时间(单位:h)随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表:
| 序号i |
分组(睡眠时间) |
频数(人数) |
频率 |
| 1 |
[4, 5) |
6 |
0.12 |
| 2 |
[5, 6) |
|
0.20 |
| 3 |
[6, 7) |
a |
|
| 4 |
[7, 8) |
b |
|
| 5 |
[8, 9) |
|
0.08 |
(1)求n值,若a=20将表中数据补全,并画出频率分布直方图
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,若据此计算的上述数据的平均值为6.52,求a, b的值,并由此估计该学校学生的日平均睡眠时间在7小时以上的频率。
(本小题满分12分)已知函数 在
在 上的最大值比最小值大2,求实数
上的最大值比最小值大2,求实数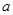 的值.
的值.
(本小题满分12分)设全集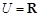 ,集合
,集合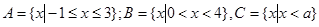
(1)求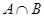 ,
,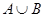 ;
;
(2)若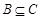 ,求实数
,求实数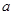 的取值范围.
的取值范围.
(本小题满分14分)一片森林原面积为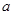 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的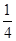 ,已知到今年为止,森林剩余面积为原的
,已知到今年为止,森林剩余面积为原的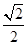 .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年;
(3)今后最多还能砍伐多少年?
(本小题满分13分)已知函数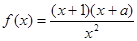 为偶函数.
为偶函数.
(1)求实数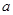 的值;
的值;
(2)记集合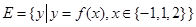 ,
,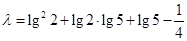 ,判断
,判断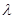 与
与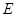 的关系;
的关系;
(3)当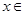
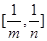
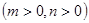 时,若函数
时,若函数 的值域为
的值域为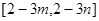 ,求
,求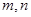 的值.
的值.
(本小题满分12分) 是定义在
是定义在 上的减函数,满足
上的减函数,满足 .
.
(1)求证: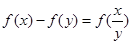 ;
;
(2)若 ,解不等式
,解不等式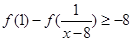 .
.