.(本题10分)中心在原点,焦点在x轴上的椭圆C上的点到焦点距离的最大值为3,最小值为1.
（1）求椭圆C的方程；
（2）若直线
与椭圆C相交于A,B两点（A,B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点.求证：直线l过定点，并求该定点的坐标.
观察（1）
;
（2）
;
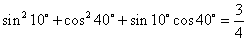（3）
.
请你根据上述规律，提出一个猜想，并证明.
有4名男生、5名女生，全体排成一行，问下列情形各有多少种不同的排法？
（Ⅰ）甲不在中间也不在两端；
（Ⅱ）甲、乙两人必须排在两端；
（Ⅲ）男、女生分别排在一起；
（Ⅳ）男女相间；
（Ⅴ）甲、乙、丙三人从左到右顺序保持一定．
（I）求函数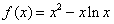
图象上的点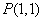
处的切线方程；
（Ⅱ）已知函数
，其中
是自然对数的底数，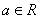
对于任意的
，
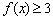恒成立，求实数
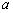的取值范围。
(9分）设x>0,y>0且x+y=1，求证：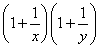
≥9.
设函数f(x)＝x3－12x＋5，x∈R.
(1)求函数f(x)的单调区间和极值；
(2)若关于x的方程f(x)＝a有三个不同实根，求实数a的取值范围；