(本小题满分10分)
已知函数y=Asin(wx+j)(A>0,w>0,0<j<p)最大值是2,最小正周期是 ,直线x=0是其图象的一条对称轴,求此函数的解析式.
,直线x=0是其图象的一条对称轴,求此函数的解析式.
在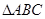 中,
中,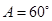 ,
,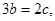
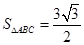 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求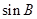 的值.
的值.
如果函数 的定义域为
的定义域为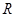 ,对于定义域内的任意
,对于定义域内的任意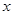 ,存在实数
,存在实数 使得
使得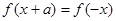 成立,则称此函数具有“
成立,则称此函数具有“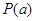 性质”.
性质”.
(1)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时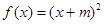 ,求
,求 在
在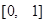 上的最大值.
上的最大值.
(2)设函数 具有“
具有“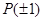 性质”,且当
性质”,且当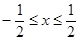 时,
时,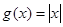 .若
.若 与
与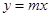 交点个数为2013个,求
交点个数为2013个,求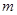 的值.
的值.
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点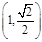
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设点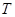
 ,过点F2作直线
,过点F2作直线 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且 ,若
,若 的取值范围
的取值范围
如图,四棱锥 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱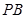 上
上
(1)求证:平面 平面
平面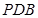 ;
;
(2)当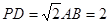 ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出 的值
的值
(本小题满分15分)设数列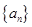 的前
的前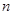 项和
项和 满足
满足 ,其中
,其中
(1)若 ,求
,求 及
及 ;
;
(2)若 ,求证:
,求证: ,并给出等号成立的充要条件
,并给出等号成立的充要条件