如果函数 的定义域为
的定义域为 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“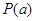 性质”.
性质”.
(1)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时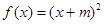 ,求
,求 在
在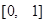 上的最大值.
上的最大值.
(2)设函数 具有“
具有“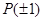 性质”,且当
性质”,且当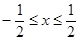 时,
时,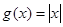 .若
.若 与
与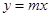 交点个数为2013个,求
交点个数为2013个,求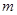 的值.
的值.
(本小题满分12分)
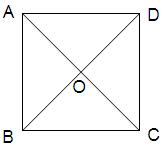
已知正方形ABCD的边长为1,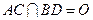 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线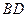 折起,使
折起,使 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.
(1)求证: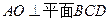 ;
;
(2)求二面角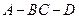 的余弦值.
的余弦值.
 |
|||||
 |
|||||
 |
|||||
(本 小题满分12分)
小题满分12分)
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别
从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为 ,“实用性”得分为
,“实用性”得分为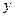 ,统计结果如下表:
,统计结果如下表:
  作品数量  |
实用性 |
|||||
| 1分 |
2分 |
3分 |
4分 |
5分 |
||
创 新 性 |
1分 |
1 |
3 |
1 |
0 |
1 |
| 2分 |
1 |
0 |
7 |
5 |
1 |
|
| 3分 |
2 |
1 |
0 |
9 |
3 |
|
| 4分 |
1 |
 |
6 |
0 |
 |
|
| 5分 |
0 |
0 |
1 |
1 |
3 |
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为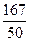 ,求
,求 、
、 的值.
的值.
已知函数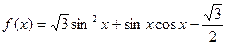
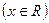 .
.
(1)若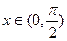 ,求
,求 的最大值;
的最大值;
(2)在 中,若
中,若 ,
, ,求
,求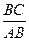 的值
的值