（本小题满分13分）
已知函数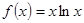
、
（Ⅰ）求函数
的单调区间；
（Ⅱ）若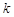
为正常数，设
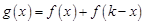，求函数
的最小值；
（Ⅲ）若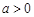
，
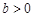，证明：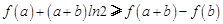
、
已知函数f(x)＝x3－x2＋
＋
.
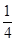证明：存在x0∈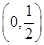
，使f(x0)＝x0.
已知f(x)＝logax(a>0且a≠1)，如果对于任意的x∈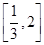
都有|f(x)|≤1成立，试求a的取值范围．
设f(x)＝loga(1＋x)＋loga(3－x)(a>0，a≠1)，且f(1)＝2.
(1)求a的值及f(x)的定义域．
(2)求f(x)在区间
上的最大值．
已知函数f(x)＝3x－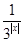
.
(1)若f(x)＝2，求x的值；
(2)判断x>0时，f(x)的单调性；
(3)若3tf(2t)＋mf(t)≥0对于t∈
恒成立，求m的取值范围．
设a>0且a≠1，函数y＝a2x＋2ax－1在[－1,1]上的最大值是14，求a的值．