已知命题 :“函数
:“函数 在
在 上单调递增。”,命题
上单调递增。”,命题 :“幂函数
:“幂函数 在
在 上单调递减”。⑴若命题
上单调递减”。⑴若命题 和命题
和命题 同时为真,求实数
同时为真,求实数 的取值范围;⑵若命题
的取值范围;⑵若命题 和命题
和命题 有且只有一个真命题,求实数
有且只有一个真命题,求实数 的取值范围。
的取值范围。
(本小题满分12分)
设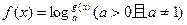
(1)若 在定义域D内是奇函数,求证:
在定义域D内是奇函数,求证: 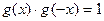 ;
;
(2)若
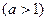 ,且在[1,3]上
,且在[1,3]上 的最大值是
的最大值是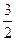 ,求实数
,求实数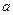 的值;
的值;
(3)在(2)的条件下,若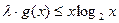 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(本小题满分 10分)
10分)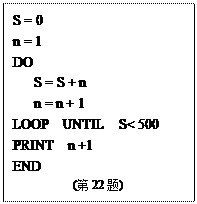
根据下面的要求,求满足 的最小的自然数
的最小的自然数 。
。
(1)画出执行该问题的程序框图;
(2)右下图是解决该问题的一个程序,但有2处错误,请找出错误并予以更正。
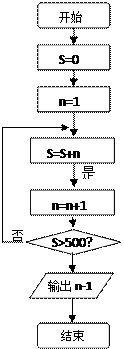 |
(本小题满分12分)
已知函数 ,
,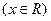 .
.
(1)用定义证明:不论 为何实数
为何实数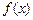 在
在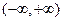 上为增函数;
上为增函数;
(2)若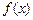 为奇函数,求
为奇函数,求 的值;
的值;
(3)在(2)的条件下,求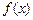 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
(本小题满分10分)
若函数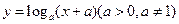 的图象过点
的图象过点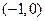 .
.
(1)求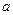 的值;
的值;
(2) 求函数的定义域.
求函数的定义域.
(本小题满分10分)
已知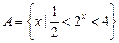 ,
, .
.
(1)求 和
和 ;
;
(2)定义运算 ,请在图中把表示“集合
,请在图中把表示“集合 ”的部分用阴影涂黑;并求
”的部分用阴影涂黑;并求 .
.