本题14分,第(1)小题6分,第(2)小题8分)
已知函数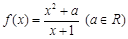 .
.
(1)用定义证明:当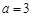 时,函数
时,函数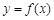 在
在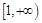 上是增函数;
上是增函数;
(2)若函数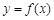 在
在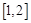 上有最小值
上有最小值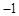 ,求实数
,求实数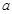 的值.
的值.
已知数列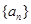 满足:
满足: ,
,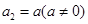 ,
, (其中
(其中 为非零常数,
为非零常数,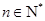 ).
).
(1)判断数列 是不是等比数列?
是不是等比数列?
(2)求 ;
;
(3)当 时,令
时,令 ,
, 为数列
为数列 的前
的前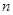 项和,求
项和,求 .
.
已知函数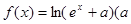 为常数,
为常数,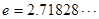 )是
)是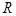 上的奇函数.
上的奇函数.
(Ⅰ)求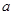 的值;(Ⅱ)讨论关于
的值;(Ⅱ)讨论关于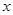 的方程
的方程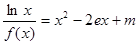 的根的个数.
的根的个数.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2 DE=2,M为AD中点.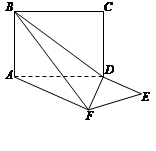
(Ⅰ) 证明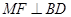 ;
;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为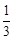 ,求AB的长.
,求AB的长.
某某种饮料每箱6听,如果其中有两听不合格产品.
(1)质检人员从中随机抽出1听,检测出不合格的概率多大?;
(2)质检人员从中随机抽出2听,设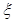 为检测出不合格产品的听数,求
为检测出不合格产品的听数,求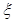 的分布列及数学期望.
的分布列及数学期望.
已知向量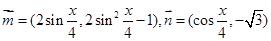 ,函数
,函数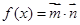 .
.
(1) 求函数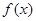 的最大值,并写出相应
的最大值,并写出相应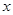 的取值集合;
的取值集合;
(2) 若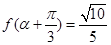 ,且
,且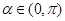 ,求
,求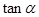 的值.
的值.