关于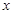 的不等式
的不等式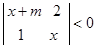 的解集为
的解集为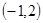 。
。
(1)求实数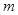 的值;
的值;
(2)若实系数一元二次方程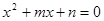 的一个根
的一个根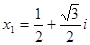 ,求
,求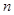 .
.
已知三个实数a、b、c成等差数列,且它们的和为12,又a+2、b+2、c+5成等比数列,求a、b、c的值。
某公司经销一种数码产品,第一年可获利200万元,从第二年起,由于市场竞争等方面的原因,其利润每年比上一年减少20万元,按照这一规律,如果公司不开发新产品,也不调整经营策略,从哪一年起,该公司经销这一产品将亏损?
某货轮在A处看灯塔B在货轮的北偏东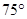 的方向上,距离为
的方向上,距离为 海里,在A处看灯塔C在货轮的北偏西
海里,在A处看灯塔C在货轮的北偏西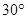 的方向上,距离为
的方向上,距离为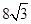 海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东
海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东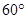 方向上,求:
方向上,求: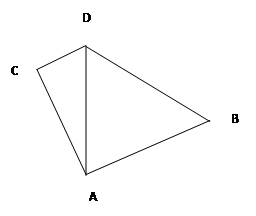
(1)AD的距离;
(2)CD的距离。
在三角形ABC中,已知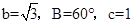 ,解三角形ABC。
,解三角形ABC。
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品在该售价的基础上每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨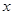 元(
元(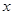 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为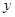 元.(14分)
元.(14分)
(1)求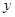 与
与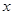 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量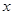 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?