、出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的。在出租车几何学中，点还是形如
的有序实数对，直线还是满足
的所有
组成的图形，角度大小的定义也和原来一样。直角坐标系内任意两点
定义它们之间的一种“距离”：
，请解决以下问题：
1、（理）求线段
上一点
的距离到原点
的“距离”；
（文）求点
、
的“距离”
；
2、（理）定义:“圆”是所有到定点“距离”为定值的点组成的图形，
求“圆周”上的所有点到点
的“距离”均为 
的“圆”方程；
（文）求线段上一点的距离到原点的“距离”；
3、（理）点、，写出线段
的垂直平分线的轨迹方程并画出大致图像．
（文）定义:“圆”是所有到定点“距离”为定值的点组成的图形，点、，
，求经过这三个点确定的一个“圆”的方程，并画出大致图像；
（说明所给图形小正方形的单位是1）
如图，已知菱形ACSB中，∠ABS=60°．沿着对角线SA将菱形ACSB折成三棱锥S﹣ABC，且在三棱锥S﹣ABC中，∠BAC=90°，O为BC中点．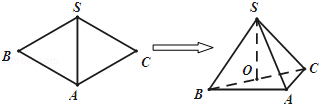
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）求平面ASC与平面SCB夹角的余弦值．
在梯形ABCD中，AD∥BC，BC=2AD，AD=AB=
，AB⊥BC，如图把△ABD沿BD翻折，使得平面ABD⊥平面BCD．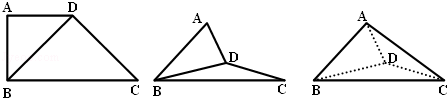
（Ⅰ）求证：CD⊥平面ABD；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离．
已知{an}是正项数列，a1=1，且点（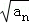
，an+1）（n∈N*）在函数y=x2+1的图象上．
（1）求数列{an}的通项公式；
（2）若列数{bn}满足b1=1，bn+1=bn+2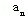
，求证：bnbn+2＜b
．
设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．
（Ⅰ）求角A的大小；
（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．
设a为实数，函数f（x）=ex﹣2x+2a，x∈R．
（1）求f（x）的单调区间及极值；
（2）求证：当a＞ln2﹣1且x＞0时，ex＞x2﹣2ax+1．