. (本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
已知公差大于零的等差数列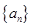 的前
的前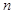 项和为
项和为 ,且满足
,且满足 ,
, ,
,
(1)求数列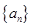 的通项公式;
的通项公式;
(2)若数列 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数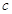 ;
;
(3)若(2)中的 的前
的前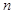 项和为
项和为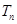 ,求证:
,求证: .
.
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知椭圆 ,常数
,常数 、
、 ,且
,且 .
.
(1) 当
当 时,过椭圆左焦点
时,过椭圆左焦点 的直线交椭圆于点
的直线交椭圆于点 ,与
,与 轴交于点
轴交于点 ,若
,若 ,求直线
,求直线 的斜率;
的斜率;
(2)过原点且斜率分别为 和
和 (
( )的两条直
)的两条直 线与椭圆
线与椭圆 的交点为
的交点为 (按逆时针顺序排列,且点
(按逆时针顺序排列,且点 位于第一象限内),试用
位于第一象限内),试用 表示四边形
表示四边形 的面积
的面积 ;
;
(3)求 的最大值.
的最大值.
(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分6分.
已知数列 满足
满足 ,
, ,
, 是数列的前
是数列的前 项和,且
项和,且 (
(
 ).
).
(1)求实数 的值;
的值;
(2)求数 列
列 的通项公式;
的通项公式; (3)对于数列
(3)对于数列 ,若存在常数M,使
,若存在常数M,使 (
( ),且
),且 ,则M叫做数列
,则M叫做数列 的“上渐近值”.
的“上渐近值”.
设 (
( ),
), 为数列
为数列 的前
的前 项和,求数列
项和,求数列 的上渐近值.
的上渐近值.
(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知函数 (
( ,
, 、
、 是常数,且
是常数,且 ),对定义域内任意
),对定义域内任意 (
( 、
、 且
且 ),恒有
),恒有 成立.
成立.
(1)求函数 的解析式,并写出函数的定义域;
的解析式,并写出函数的定义域;
(2)求 的取值范围,使得
的取值范围,使得 .
.
本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知△ 的周长为
的周长为 ,且
,且 .
.
(1)求边长 的值;
的值;
(2)若 (结果用反三角函数值表示).
(结果用反三角函数值表示).
本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知长方体 ,
, ,点M是棱
,点M是棱 的中点.
的中点.
(1)试用反证法证明 直线
直线 是异面直线;
是异面直线;
(2)求直线 所成的角(结果用反三角函数值表示).
所成的角(结果用反三角函数值表示).