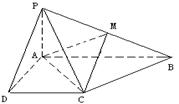
(满分12分)已知四棱锥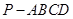 的底面为直角梯形,
的底面为直角梯形,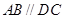 ,
,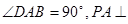 底面
底面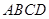 ,且
,且 ,
,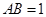 ,
, 是
是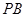 的中点。
的中点。
(Ⅰ)证明:面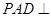 面
面 ;
;
(Ⅱ)求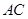 与
与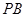 所成的角;
所成的角;
(Ⅲ)求面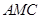 与面
与面 所成二面角的余弦值。
所成二面角的余弦值。
(本小题满分14分)已知 是二次函数,不等式
是二次函数,不等式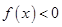 的解集是
的解集是 ,且
,且 在区间
在区间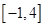 上的最大值是
上的最大值是 .
.
(1)求 的解析式;
的解析式;
(2)设函数 在
在 上的最小值为
上的最小值为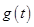 ,求
,求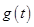 的表达式.
的表达式.
(本小题满分14分)
已知向量 ,
,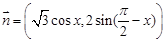 ,函数
,函数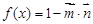 .
.
(1)求函数 的解析式;
的解析式;
(2)当 时,求
时,求 的单调递增区间;
的单调递增区间;
(3)说明 的图象可以由
的图象可以由 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
(本小题满分12分)在△ 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 ,若
,若 ,且
,且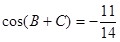 .
.
(1)求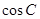 的值; (2)若
的值; (2)若 ,求△
,求△ 的面积.
的面积.
(本小题满分14分)文科班某同学参加广东省学业水平测试,物理、化学、生物获得等级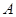 和获得等级不是
和获得等级不是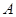 的机会相等,物理、化学、生物获得等级
的机会相等,物理、化学、生物获得等级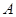 的事件分别记为
的事件分别记为 、
、 、
、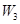 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是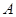 的事件分别记为
的事件分别记为 、
、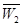 、
、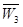 .
.
(1)试列举该同学这次水平测试中物理、化学、生物成绩是否为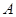 的所有可能结果(如三科成绩均为
的所有可能结果(如三科成绩均为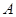 记为
记为 );
);
(2)求该同学参加这次水平测试获得两个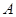 的概率;
的概率;
(3)试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件,使该事件的概率大于 ,并说明理由.
,并说明理由.
(本小题满分12分)
已知函数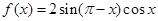 .
.
(1)求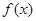 的最小正周期;(2)求
的最小正周期;(2)求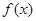 的最大值及取得最大值时
的最大值及取得最大值时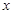 的集合.
的集合.