设函数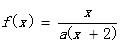 方程f(x)=x有唯一的解,
方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且
(1)求证:数列{ }是等差数列;
}是等差数列;
(2)若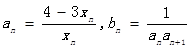 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn;
(3)在(2)的冬件下,若不等式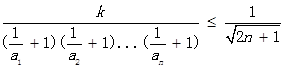 对一切n∈N﹡
对一切n∈N﹡
均成立,求k的最大值.
( 本小题满分12分) 在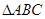 中,内角
中,内角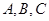 的对边分别为
的对边分别为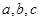 ,且
,且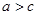 .已知
.已知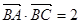 ,
,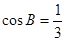 ,
, 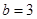 .求:
.求:
(1)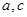 的值;
的值;
(2)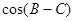 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
已知函数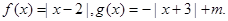
(1) 解关于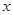 的不等式
的不等式 ;
;
(2) 若函数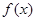 的图象恒在函数
的图象恒在函数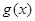 图象的上方,求
图象的上方,求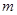 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线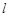 的参数方程是
的参数方程是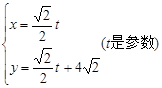 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.
(1)求圆心C的直角坐标;
(2)由直线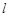 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
(本小题满分10分)选修4-1:几何证明选讲
如图,⊙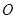 的直径
的直径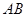 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点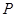 ,
,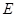 为⊙
为⊙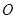 上一点,AE=AC ,
上一点,AE=AC ,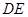 交
交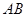 于点
于点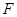 ,且
,且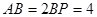 ,
,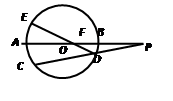
(Ⅰ)求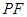 的长度.
的长度.
(Ⅱ)若圆F与圆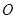 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
(本小题满分12分)已知函数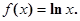
(1)若直线 是曲线
是曲线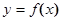 的切线,求
的切线,求 的值;
的值;
(2)若直线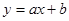 是曲线
是曲线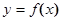 的切线,求
的切线,求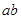 的最大值;
的最大值;
(3)设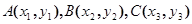 是曲线
是曲线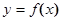 上相异三点,其中
上相异三点,其中 求证:
求证: