(本小题满分14分)已知椭圆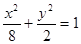 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
(1)当 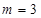 时,判断直线l与椭圆的位置关系;
时,判断直线l与椭圆的位置关系;
(2)当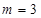 时,P为椭圆上的动点,求点P到直线l距离的最小值;
时,P为椭圆上的动点,求点P到直线l距离的最小值;
(3)如图,当l交椭圆于A、B两个不同点时,求证:
直线MA、MB与x轴始终围成一个等腰三角形 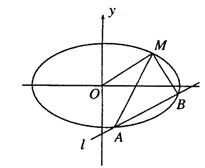
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.
(1)求 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取 个元件,元件寿命落在
个元件,元件寿命落在 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在 之间,一个元件寿命落在
之间,一个元件寿命落在 之间”的概率.
之间”的概率.
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列
,数列 的首项
的首项 ,
, .
.
(1)求函数 的表达式;(2)求数列
的表达式;(2)求数列 的前
的前 项和
项和 .
.
设函数 .
.
(1)若不等式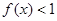 的解集为
的解集为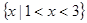 ,求
,求 的值;
的值;
(2)若存在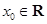 ,使
,使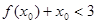 ,求
,求 的取值范围.
的取值范围.
已知直线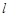 的参数方程为
的参数方程为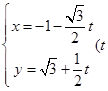 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,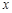 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆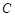 的极坐标方程为
的极坐标方程为 .
.
(1)求圆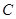 的直角坐标方程;
的直角坐标方程;
(2)若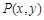 是直线
是直线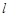 与圆面
与圆面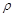 ≤
≤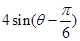 的公共点,求
的公共点,求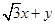 的取值范围.
的取值范围.
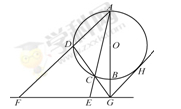
如图,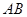 是圆
是圆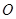 的直径,
的直径, 是
是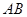 延长线上的一点,
延长线上的一点,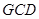 是圆
是圆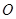 的割线,过点
的割线,过点 作
作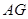 的垂线,交直线
的垂线,交直线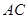 于点
于点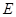 ,交直线
,交直线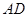 于点
于点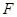 ,过点
,过点 作圆
作圆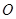 的切线,切点为
的切线,切点为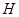 .
.
(1)求证: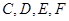 四点共圆;(2)若
四点共圆;(2)若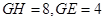 ,求
,求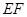 的长.
的长.