(本小题满分13分)
已知命题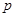 :方程
:方程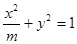 表示焦点在y轴上的椭圆; 命题
表示焦点在y轴上的椭圆; 命题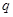 :直线
:直线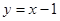
与抛物线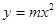 有两个交点
有两个交点
(I)若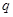 为真命题,求实数
为真命题,求实数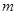 的取值范围
的取值范围
(II)若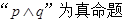 ,求实数
,求实数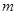 的取值范围。
的取值范围。
直线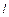 过曲线
过曲线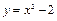 上一点
上一点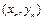 ,斜率为
,斜率为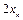 ,且
,且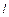 与x轴交于点
与x轴交于点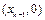 ,其中
,其中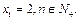
⑴试用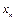 表示
表示 ;
;
⑵证明: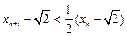 ;
;
⑶若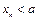 对
对 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
已知 是定义在
是定义在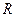 上的奇函数,当
上的奇函数,当 时,
时,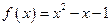 。
。
(1)求函数 的解析式;
的解析式;
(2)求不等式 的解集。
的解集。
已知双曲线的中心在原点,右顶点为A(1,0),点P、Q在双曲线的右支上,点M(m,0)到直线AP的距离为1.
(1)若直线AP的斜率为k,且|k|∈[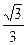 ,
, ],求实数m的取值范围;
],求实数m的取值范围;
(2)当m= +1时,△APQ的内心恰好是点M,求此双曲线的方程.
+1时,△APQ的内心恰好是点M,求此双曲线的方程.
已知双曲线x2-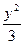 =1,双曲线存在关于直线l:y=kx+4的对称点,求实数k的取值范围.
=1,双曲线存在关于直线l:y=kx+4的对称点,求实数k的取值范围.
如图,双曲线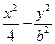 =1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.
=1(b∈N*)的两个焦点为F1、F2,P为双曲线上一点,|OP|<5,|PF1|、|F1F2|、|PF2|成等差数列,求此双曲线方程.