(本小题满分12分)
某射击运动员进行射击训练,前三次射击在靶上的着弹点 刚好是边长为
刚好是边长为 的等边三角形的三个顶点.
的等边三角形的三个顶点.
(Ⅰ)第四次射击时,该运动员瞄准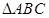 区域射击(不会打到
区域射击(不会打到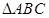 外),则此次射击的着弹点距
外),则此次射击的着弹点距 的距离都超过
的距离都超过 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间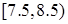 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间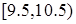 内.现从这
内.现从这 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为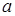 和
和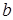 )进行技术分析.求事件“
)进行技术分析.求事件“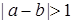 ”的概率.
”的概率. 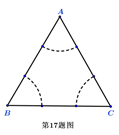
设数列 满足
满足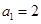 ,
,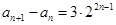
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令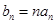 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知函数
(Ⅰ)若对任意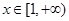 ,使得
,使得 恒成立,求实数
恒成立,求实数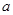 的取值范围;
的取值范围;
(Ⅱ)证明:对 ,不等式
,不等式 成立.
成立.
设点A( ,0),B(
,0),B( ,0),直线AM、BM相交于点M,且它们的斜率之积为
,0),直线AM、BM相交于点M,且它们的斜率之积为 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)若直线 过点F(1,0)且绕F旋转,
过点F(1,0)且绕F旋转, 与圆
与圆 相交于P、Q两点,
相交于P、Q两点, 与轨迹C相交于R、S两点,若|PQ|
与轨迹C相交于R、S两点,若|PQ|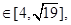 求△
求△ 的面积的最大值和最小值(F′为轨迹C的左焦点).
的面积的最大值和最小值(F′为轨迹C的左焦点).
正方形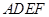 与梯形
与梯形 所在平面互相垂直,
所在平面互相垂直,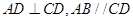 ,
,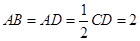 ,点
,点 在线段
在线段 上且不与
上且不与 重合。
重合。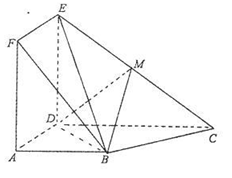
(Ⅰ)当点M是EC中点时,求证:BM//平面ADEF;
(Ⅱ)当平面BDM与平面ABF所成锐二面角的余弦值为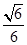 时,求三棱锥
时,求三棱锥 的体积.
的体积.
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求摸2次恰好第2次中奖的概率;
(Ⅱ)每次同时摸2个,并放回,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).