为了测量某住宅大楼每层的平均高度(层高)及电梯运行情况,甲、乙两位同学在一楼电梯内用电子体重计及秒表进行了以下实验,一质量为m=50kg的甲同学站在体重计上,乙同学记录电梯从地面一楼到顶层全过程中,体重计示数随时间变化的情况,并作出了如图所示的图像,已知t=0时,电梯静止不动,从电梯内楼层按钮上获知该大楼共19层.求:
电梯启动和制动时的加速度大小;
该大楼的层高.
右图电路中 ,滑动变阻器R3上标有“20 Ω,2 A”字样,理想电压表的量程有0~3 V和0~15 V两挡,理想电流表的量程有0~0.6 A和0~3 A两挡.闭合开关S,将滑片P从最左端向右移动到某位置时,电压表、电流表示数分别为2.5 V和0.3 A;继续向右移动滑片P至另一位置,电压表指针指在满偏的
,滑动变阻器R3上标有“20 Ω,2 A”字样,理想电压表的量程有0~3 V和0~15 V两挡,理想电流表的量程有0~0.6 A和0~3 A两挡.闭合开关S,将滑片P从最左端向右移动到某位置时,电压表、电流表示数分别为2.5 V和0.3 A;继续向右移动滑片P至另一位置,电压表指针指在满偏的 ,电流表指针指在满偏的
,电流表指针指在满偏的 ,求:
,求:
(1)此时电流表示数;
(2)电源的电动势.
如图1所示,宽度为d的竖直狭长区域内(边界为 ),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为
),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为 ,
, 表示电场方向竖直向上.t=0时,一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域,沿直线运动到Q点后,做一次完整的圆周运动,再沿直线运动到右边界上的N2点.Q为线段
表示电场方向竖直向上.t=0时,一带正电、质量为m的微粒从左边界上的N1点以水平速度v射入该区域,沿直线运动到Q点后,做一次完整的圆周运动,再沿直线运动到右边界上的N2点.Q为线段 的中点,重力加速度为g.上述d、
的中点,重力加速度为g.上述d、 、m、v、g为已知量.
、m、v、g为已知量.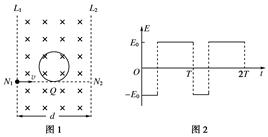
(1)求微粒所带电荷量q和磁感应强度B的大小;
(2)求电场变化的周期T;
(3)改变宽度d,使微粒仍能按上述运动过程通过相应宽度的区域,求T的最小值.
如右图所示为研究带电粒子在磁场中偏转问题的实验装置:M、N是竖直放置的两正对着的平行金属板,S1、S2是板上两个正对的小孔,其中N板的右侧有一个在竖直面内,以O为圆心的圆形区域,该区域内存在垂直圆面向外的匀强磁场,另有一个同样以O为圆心的半圆形荧光屏AO′C.已知S1、S2、O和荧光屏的中间位置O′在同一直线上,且AC⊥S1O′.当在M、N板间加恒定电压U时,一带正电离子在S1处由静止开始加速向S2孔运动,最后打在图示的荧光屏上的P处,∠COP=30°.若要让上述带正电离子(不计重力)仍在S1处由静止开始加速,最后打在图示的荧光屏下边缘C处,求M、N板间所加电压的大小U′.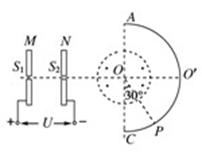
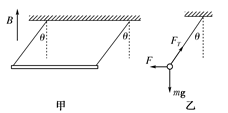
如图甲所示,质量为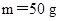 ,长
,长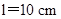 的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度
的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度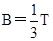 .未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度
.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度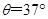 ,求此棒中恒定电流的大小.
,求此棒中恒定电流的大小.
某同学对棒中恒定电流的解法如下:对铜棒进行受力分析,通电时导线向外偏转,说明安培力方向垂直电流和磁场方向向外,受力如图乙所示(侧视图).
当最大偏转角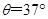 时,棒受力平衡.有
时,棒受力平衡.有 ,得
,得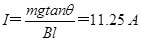 .
.
(1)请判断,该同学的解法正确吗?若不正确则请指出错在哪里?
(2)试写出求解棒中电流的正确解答过程及结果.
如右图所示,楼梯口一倾斜天花板与水平面的夹角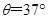 ,一装潢工人手持木杆绑着刷子粉刷天花板.工人所持木杆对刷子的作用力始终保持竖直向上,大小为
,一装潢工人手持木杆绑着刷子粉刷天花板.工人所持木杆对刷子的作用力始终保持竖直向上,大小为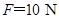 ,刷子的质量为
,刷子的质量为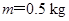 ,刷子可视为质点,且沿天花板向上匀速运动,取
,刷子可视为质点,且沿天花板向上匀速运动,取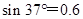 ,试求刷子与天花板间的动摩擦因数.
,试求刷子与天花板间的动摩擦因数.