已知数列{an}的前n项和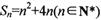
，数列
为等比数列，且首项b1和公比q满足：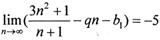
(I)求数列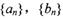
的通项公式;
(II)设
，记数列
的前n项和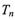
，若不等式
对任意
恒成立,求实数
的最大值.
如图，四棱锥S—ABCD的底面为正方形，SD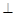
底面ABCD，则下列结论中不正确的是（）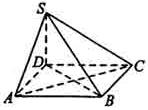
| A．AC⊥SB |
| B．AB∥平面SCD |
| C．SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D．AB与SC所成的角等于DC与SA所成的角 |
张华同学上学途中必须经过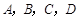
四个交通岗，其中在
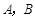岗遇到红灯的概率均为
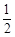，在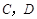
岗遇到红灯的概率均为
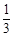．假设他在4个交通岗遇到红灯的事件是相互独立的，X表示他遇到红灯的次数．
（1）若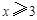
，就会迟到，求张华不迟到的概率；
（2）求EX．
甲、乙、丙三名射击选手，各射击一次，击中目标的概率如下表所示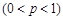
：
| 选手 |
甲 |
乙 |
丙 |
| 概率 |
 |
 |
|
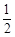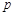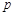若三人各射击一次，恰有k名选手击中目标的概率记为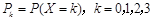
．
（1）求X的分布列；
（2）若击中目标人数的均值是2，求P的值．
掷3枚均匀硬币一次，求正面个数与反面个数之差X的分布列，并求其均值。
从1到9的九个数字中取三个偶数四个奇数，试问：
①能组成多少个没有重复数字的七位数？
②上述七位数中三个偶数排在一起的有几个？
③在①中的七位数中，偶数排在一起、奇数也排在一起的有几个？
④在①中任意两偶然都不相邻的七位数有几个？