.(本小题满分14分)
已知数列{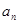 }满足
}满足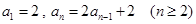 .
.
(1)证明:数列{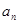 +2}是等比数列.并求数列{
+2}是等比数列.并求数列{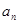 }的通项公式
}的通项公式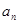 ;
;
(2)若数列{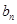 }满足
}满足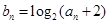 ,设
,设 是数列
是数列 的前n项和.
的前n项和.
求证: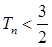
(本小题满分8分)已知向量 ,
,  的夹角为
的夹角为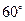 , 且
, 且 ,
,  ,
,
(1) 求 ; (2) 求
; (2) 求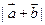 .
.
(本小题满分8分)
(1)已知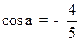 ,且
,且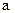 为第三象限角,求
为第三象限角,求 的值
的值
(2)已知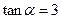 ,计算
,计算 的值
的值
(本小题满分14分)
已知动圆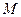 过定点
过定点 ,且与定直线
,且与定直线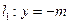 相切,动圆圆心
相切,动圆圆心
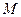 的轨迹为
的轨迹为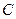 ,直线
,直线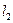 过点
过点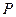 交曲线
交曲线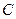 于
于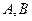 两点.
两点.
(Ⅰ)求曲线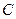 的方程;
的方程;
(Ⅱ)若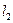 交
交 轴于点
轴于点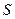 ,且
,且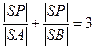 ,求
,求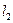 的方程;
的方程;
(Ⅲ)若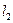 的倾斜角为
的倾斜角为 ,在
,在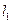 上是否存在点
上是否存在点 使
使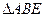 为正三角形? 若能,求点
为正三角形? 若能,求点 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
(本小题满分12分)
已知函数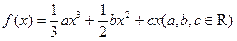 在点
在点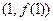 处的切线斜率为
处的切线斜率为 ,且
,且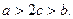
(Ⅰ)证明: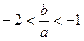 ; (Ⅱ)证明:函数
; (Ⅱ)证明:函数 在区间
在区间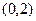 内至少有一个极值点.
内至少有一个极值点.
(本小题满分12分)
已知函数 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式及
的通项公式及 的最大值;
的最大值;
(Ⅱ)令 ,其中
,其中 ,求
,求 的前
的前 项和.
项和.