.已知双曲线G的中心在原点,它的渐近线与圆x2+y2-10x+20=0相切.过点P(-4,0)作斜率为的直线 ,使得
,使得 和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|=|PC|2.
和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|=|PC|2.
(1)求双曲线G的渐近线的方程;
(2)求双曲线G的方程;
(3)椭圆S的中心在原点,它的短轴是G的实轴.如果S中垂直于 的平行弦的中点的轨迹恰好是G的渐近线截在S内的部分AB,若P(x,y)(y>0)为椭圆上一点,求当
的平行弦的中点的轨迹恰好是G的渐近线截在S内的部分AB,若P(x,y)(y>0)为椭圆上一点,求当 的面积最大时点P的坐标.
的面积最大时点P的坐标.
已知 分别是
分别是 的三个内角
的三个内角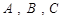 的对边,
的对边,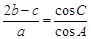 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求函数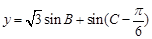 的值域.
的值域.
命题 :不等式
:不等式 对一切实数
对一切实数 都成立;命题
都成立;命题 :已知函数
:已知函数 的图像在点
的图像在点 处的切线恰好与直线
处的切线恰好与直线 平行,且
平行,且 在
在 上单调递减.若命题
上单调递减.若命题 或
或 为真,求实数
为真,求实数 的取值范围.
的取值范围.
已知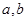 是正实数,设函数
是正实数,设函数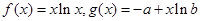 。
。
(Ⅰ)设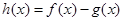 ,求
,求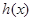 的单调区间;
的单调区间;
(Ⅱ)若存在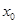 ,使
,使 且
且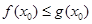 成立,求
成立,求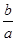 的取值范围。
的取值范围。
已知数列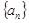 满足
满足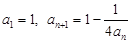 ,其中
,其中 N*.
N*.
(Ⅰ)设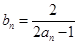 ,求证:数列
,求证:数列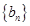 是等差数列,并求出
是等差数列,并求出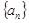 的通项公式
的通项公式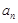 ;
;
(Ⅱ)设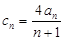 ,数列
,数列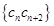 的前
的前 项和为
项和为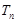 ,是否存在正整数
,是否存在正整数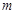 ,使得
,使得 对于
对于 N*恒成立,若存在,求出
N*恒成立,若存在,求出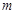 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
在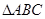 中,
中,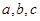 分别为角
分别为角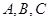 所对的边,向量
所对的边,向量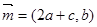 ,
, 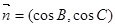 ,且
,且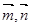 垂直.
垂直.
(Ⅰ)确定角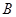 的大小;
的大小;
(Ⅱ)若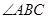 的平分线
的平分线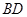 交
交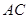 于点
于点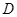 ,且
,且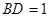 ,设
,设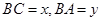 ,试确定
,试确定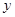 关于
关于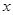 的函数式,并求边
的函数式,并求边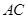 长的取值范围.
长的取值范围.