已知函数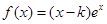 .
.
(1)求 的单调区间;
的单调区间;
(2)求 在区间
在区间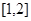 上的最小值;
上的最小值;
(3)设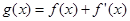 ,当
,当 时,对任意
时,对任意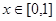 ,都有
,都有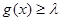 成立,求实数
成立,求实数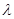 的取值范围。
的取值范围。
某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数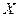 的概率分布
的概率分布
个袋中有6个同样大小的黑球,编好为1,2,3,4,5,6,现从中随机取出3个球,以X表示取出球的最大号码,求X的概率分布列
甲、乙两名篮球运动员,甲投篮的命中率为0.6,乙投篮的命中率为0.7,两人是否投中相互之间没有影响,求:
(1)两人各投一次,只有一人命中的概率;
(2)每人投篮两次,甲投中1球且乙投中2球的概率.
求二项式(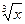 -
-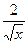 )15的展开式中:
)15的展开式中:
(1)常数项;
(2)有几个有理项;
现有5名男生和3名女生.
(1)若3名女生必须相邻排在一起,则这8人站成一排,共有多少种不同的排法?
(2)若从中选5人,且要求女生只有2名, 站成一排,共有多少种不同的排法?