已知函数
(Ⅰ)求 与
与 ,
, 与
与 ;
;
(Ⅱ)由(Ⅰ)中求得结果,你能发现当 时,
时, 与
与 有什么关系?并证明你的发现;
有什么关系?并证明你的发现;
(Ⅲ)求 .
.
(12分)用简单随机抽样从含有8个个体的总体中抽取一个容量为2的样本.问:
①总体中的某一个体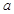 在第一次抽取时被抽到的概率是多少?
在第一次抽取时被抽到的概率是多少?
②个体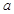 在第1次未被抽到,而第2次被抽到的概率是多少?
在第1次未被抽到,而第2次被抽到的概率是多少?
③在整个抽样过程中,个体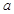 被抽到的概率是多少?
被抽到的概率是多少?
(10分)有10件产品,其中有2件次品,从中随机抽取3件,求:
(1)其中恰有1件次品的概率;(2)至少有一件次品的概率、
(本小题满分14分)设 .
.
(1)若函数 在区间
在区间 内单调递减,求
内单调递减,求 的取值范围;
的取值范围;
(2) 若函数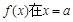 处取得极小值是
处取得极小值是 ,求
,求 的值,并说明在区间
的值,并说明在区间 内函数
内函数
的单调性.
(本小题满分14分)设椭圆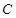 :
: 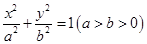 过点(0,4),离心率为
过点(0,4),离心率为 .
.
(1)求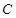 的方程;
的方程;
(2)求过点(3,0)且斜率为 的直线被
的直线被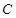 所截线段的中点坐标.
所截线段的中点坐标.
(本小题满分14分)如图,一简单几何体有五个顶点 、
、 、
、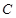 、
、 、
、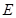 ,它的一个面
,它的一个面 内接于⊙
内接于⊙ ,
,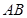 是⊙
是⊙ 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形,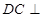 平面
平面 .
.
(1)证明:平面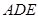
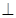 平面
平面 ;
;
(2)若 ,
,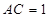 ,
,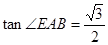 ,求该简单几何体的体积.
,求该简单几何体的体积.