某公园准备建一个摩天轮,摩天轮的外围是一个周长为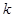 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为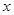 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为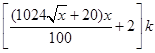 元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为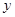 元.
元.
(Ⅰ)试写出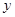 关于
关于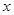 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(Ⅱ)当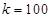 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?
(本题12分)已知椭圆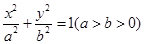 的离心率
的离心率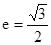 ,过
,过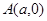 、
、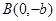 两点的直线到原点的距离是
两点的直线到原点的距离是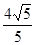 .
.
(1)求椭圆的方程 ;
(2)已知直线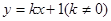 交椭圆于不同的两点
交椭圆于不同的两点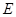 、
、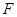 ,且
,且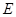 、
、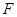 都在以
都在以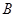 为圆心的圆上,求
为圆心的圆上,求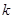 的值.
的值.
(本题12分)已知中心在原点的双曲线的右焦点为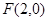 ,右顶点为
,右顶点为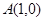 .
.
(1)试求双曲线的方程;
(2)过左焦点作倾斜角为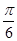 的弦
的弦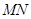 ,试求
,试求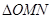 的面积(
的面积(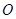 为坐标原点).
为坐标原点).
(本题12分)已知命题 :方程
:方程 表示焦点在
表示焦点在 轴上的椭圆;命题
轴上的椭圆;命题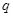 :点
:点 在圆
在圆 内.若
内.若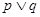 为真命题,
为真命题, 为假命题,试求实数
为假命题,试求实数 的取值范围.
的取值范围.
(本题12分)已知椭圆的焦点是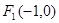 和
和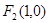 ,又过点
,又过点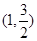 .
.
(1)求椭圆的离心率;
(2)又设点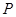 在这个椭圆上,且
在这个椭圆上,且 ,求
,求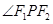 的余弦的大小.
的余弦的大小.
(本题10分)圆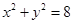 内一点
内一点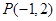 ,过点
,过点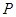 的直线
的直线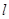 的倾斜角为
的倾斜角为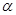 ,直线
,直线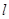 交圆于
交圆于 两点.
两点.
⑴当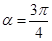 时,求弦
时,求弦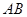 的长;
的长;
⑵当弦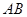 被点
被点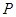 平分时,求直线
平分时,求直线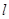 的方程.
的方程.