(本大题15分)
甲、乙两人在300米的环形跑道上练习长跑,甲的速度是6米/秒,乙的速度是7米/秒.如果甲、乙两人同地背向跑,乙先跑2秒,那么再经过多少秒两人相遇?
如果甲、乙两人同时同地同向跑,乙跑几圈后能首次追上甲?
如果甲、乙两人同时同向跑,乙在甲前面6米,经过多少
 秒后两人第二次相遇?
秒后两人第二次相遇?
如图是1710的正方形网格,四边形ABCD的四个顶点都在网格的顶点上,我们把这样的四边形称作格点四边形.请在网格中画出一个与四边形ABCD相似但不全等的格点四边形EFGH.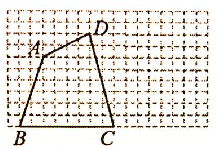
如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.
(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE.
(2)如图2,当点D在线段BC延长线上时,探究AD、BD、CD三条线段之间的数量关系,写出结论并说明理由;
(3)若BD= CD,直接写出∠BAD的度数.
CD,直接写出∠BAD的度数.
某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
| x |
30 |
32 |
34 |
36 |
| y |
40 |
36 |
32 |
28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,若BC:AB=3:4,求线段CD的长.