．
如图，在平面直角坐标系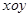
中，点
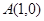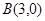，点
，点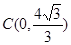
，直线经过点
，
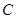（1）若在
轴上
方直线
上存在点
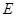使△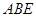
为等边三角形，求直线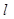所表达的函数关系式；（2）若在
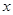轴上方直线上有且只有
三个点能和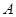
、
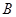构成直角三角形，求直线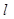所表达的函数关系式；（3）若在
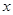轴上方直线上有且只有一个点在函数
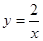的图形上，求直线所表达的函数关系式.
学校为统筹安排大课间体育活动，在各班随机选取了一部分学生，分成四类活动：“篮球”、 “羽毛球”、 “乒乓球”、“其他”进行调查，整理收集到的数据，绘制成如下的两幅统计图．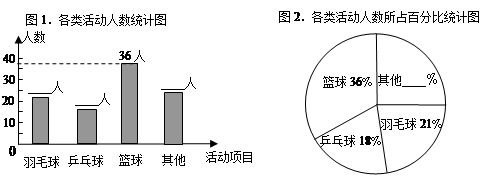
（1）学校采用的调查方式是；学校在各班共随机选取了名学生；
（2）补全统计图中的数据：羽毛球人、乒乓球人、其他人、其他﹪；
（3）该校共有1100名学生，请计算喜欢“篮球”的学生人数．
已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．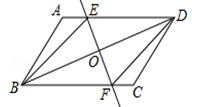
（1）求证：OE=OF．
（2）当∠DOE等于度时，四边形BFDE为菱形．（直接填写答案即可）
在边长为1的小正方形网格中，△AOB的顶点均在格点上．
（1）B点关于y轴的对称点坐标为；
（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；
（3）在（2）的条件下，A1的坐标为．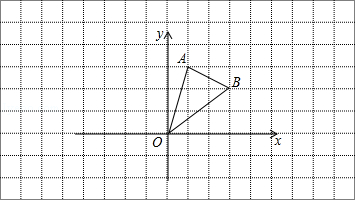
化简：
解方程：