如图,四边形 是正方形,点 , 分别在 , 上,且 .
求证: .
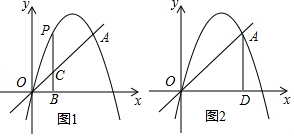
已知:如图,抛物线 经过原点 和点 , 为抛物线上的一个动点,过点 作 轴的垂线,垂足为 ,并与直线 交于点 .
(1)求抛物线的解析式;
(2)当点 在直线 上方时,求线段 的最大值;
(3)过点 作 轴于点 ,在抛物线上是否存在点 ,使得以 、 、 、 四点为顶点的四边形是平行四边形?若存在,求 的值;若不存在,请说明理由.
如图, 为 的直径, 为 的弦, ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

如图,两建筑物的水平距离 为 ,从 点分别测得 点的俯角为 、 点的俯角为 ,求这两建筑物的高度 和 .

列分式方程解应用题:
已知一台机器每小时磨青稞的质量比一个人每小时手工磨青稞的10倍还多 ,这台机器磨 青稞所用的时间和这个人手工磨 青稞所用的时间相同,求这个人每小时手工磨青稞多少千克?