某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用该药，第一次服药后每毫升血液中的含药
量
与服药后的时间
之间近似满足如图所示的曲线。其中
是直线段，曲线部分是过
、
两点的函数
的图象。
（I）写出第一次服药后每毫升血液中含药量
关于时间
的函数关系式；
（II）据测定：每毫升血液中含药量不少于
时治疗有效，假若某病人第一次服药为早上6:00，为保持疗效，第二次服药最迟是当天几点钟？
(Ⅲ) 若按（II）中的最迟时间服用第二次药，则第二次服药后再过
，该病人每毫升血液中含药量为多少
？（精确到
）。
已知f(x)是R上的奇函数，且当x∈(-∞,0)时，f(x)=-xlg(2-x),求f(x)的解析式.
已知f(x)是实数集R上的函数，且对任意x
R,f(x)=f(x+1)+f(x-1)恒成立.
(1)求证：f(x)是周期函数.
(2)已知f(3)=2，求f(2 004).
已知函数y=f(x)的定义域为R，且对任意a,b∈R,都有f(a+b)=f(a)+f(b)，且当x＞0时，f(x)＜0恒成立，f(3)="-3."
(1)证明：函数y=f(x)是R上的减函数；
（2）证明：函数y=f(x)是奇函数；
（3）试求函数y=f(x)在［m,n］（m,n∈Z）上的值域.
判断下列各函数的奇偶性：
（1）f（x）=（x-2）
；
（2）f（x）=
；
（3）f（x）=
已知函数f(x)的定义域为R，且满足f(x+2)=-f(x).
（1）求证：f(x)是周期函数；
（2）若f(x)为奇函数，且当0≤x≤1时，f(x)=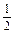
x,求使f(x)=-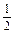在［0，2 009］上的所有x的个数.