(本题12分) 抛物线的顶点在原点,焦点在射线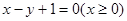
 上
上
(1)求抛物线的标准方程;
(2)过(1)中抛物线的焦点F作动弦AB,过A、B两点分别作抛物线的切线,设其交点为M,求点M的轨迹方程,并求出 的值.
的值.
记函数 的定义域为集合
的定义域为集合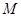 ,函数
,函数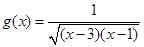 的定义域为集合
的定义域为集合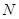 .求:
.求:
(Ⅰ)集合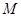 ,
,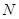 ;
;
(Ⅱ)集合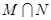 ,
,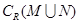 .
.
假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间
(1)你离家前不能看到报纸(称事件A)的概率是多少?(6分,须有过程)
(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)
(本小题满分12分)在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
下面是计算应纳税所得额的算法过程,其算法如下:
第一步输入工资x(注x<=5000);
第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);
否则 y=25+0.1(x-1300)
第三步输出税款y, 结束。
请写出该算法的程序框图和程序。(注意:程序框图与程序必须对应)
为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:请判断:谁参加这项重大比赛更合适,并阐述理由。
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |