为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:请判断:谁参加这项重大比赛更合适,并阐述理由。
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(本题满分15分) 已知函数f(x)= x3+ax2+bx,a , b
x3+ax2+bx,a , b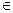 R.
R.
(Ⅰ) 曲线C:y=f(x) 经过点P(1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(Ⅱ) 已知f(x)在区间(1,2) 内存在两个极值点,求证:0<a+b<2
(本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为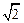 .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
(本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,
前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明: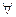 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
(本题满分14分) 设向量α=(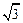 sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f(x)=α
sin 2x,sin x+cos x),β=(1,sin x-cos x),其中x∈R,函数f(x)=α β.
β.
(Ⅰ) 求f(x)的最小正周期;
(Ⅱ) 若f(θ)=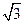 ,其中0<θ<
,其中0<θ<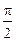 ,求cos(θ+
,求cos(θ+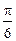 )的值.
)的值.
已知函数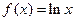 ,
,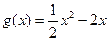
(1) 设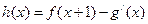 (其中
(其中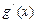 是
是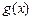 的导函数),求
的导函数),求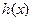 的最大值;
的最大值;
(2) 证明: 当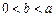 时,求证:
时,求证: ;
;
(3) 设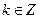 ,当
,当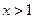 时,不等式
时,不等式 恒成立,求
恒成立,求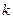 的最大值
的最大值