（本小题满分9分）甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图表．
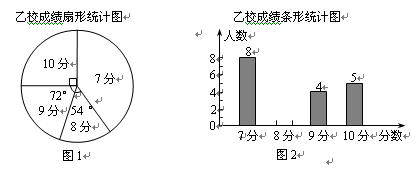
（1）在图1中，“7分”所在扇形的圆心角等于 °．
（2）请你将图2的统计图补充完整．
（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好．
（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？
如图，⊙O的直径AB＝12cm，AM和BN是它的两条切线，DE切⊙O于E，交AM于D，交BN于C
（1）若AD＝4cm，求BC的长；
（2）设AD=x，BC=y，求y与x的函数关系式；
（3）梯形ABCD的面积为78cm2，求AD的长
一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1
个单位．用实数加法表示为 3+（
）=1．若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移
个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移
个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为 
．
（1）计算：{3，1}+{1，2}；
（2）动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”{3，1}平移，最后的位置还是点O吗? 在图1中画出四边形OABC.
（3）如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O. 请用“平移量”加法算式表示它的航行过程．
李晖到“宇泉牌”服装专卖店做社会调查．了解到商店为了激励营业员的工作积极性，实行“月总收入＝基本工资＋计件奖金”的方法，并获得如下信息：
| 营业员 |
小俐 |
小花 |
| 月销售件数（件） |
200 |
150 |
| 月总收入（元） |
1400 |
1250 |
假设月销售件数为
件，月总收入为
元，销售每件奖励
元，营业员月基本工资为
元．
（1）求
的值；
（2）若营业员小俐某月总收入不低于
元，那么小俐当月至少要卖服装多少件？
一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为
，两车之间的距离为
，图中的折线表示
与
之间的函数关系．根据图象进行以下探究：
信息读取：
（1）甲、乙两地之间的距离为km；
（2）请解释图中点
的实际意义；
图象理解：
（3）求慢车和快车的速度；
（4）求线段
所表示的与之间的函数关系式，并写出自变量的取值范围；
问题解决：
（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？
某加油站五月份营销一种油品的销售利润
（万元）与销售量
（万升）之间函数关系的图象如图中折线所示，该加油站截止到13日调价时的销售利润为4万元，截止至15日进油时的销售利润为5.5万元．（销售利润＝（售价－成本价）×销售量）
请你根据图象及加油站五月份该油品的所有销售记录提供的信息，解答下列问题：
（1）求销售量为多少时，销售利润为4万元；
（2）分别求出线段AB与BC所对应的函数关系式；
（3）我们把销售每升油所获得的利润称为利润率，那么，在OA、AB、BC三段所表示的销售信息中，哪一段的利润率最大？（直接写出答案）