一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1
个单位.用实数加法表示为 3+(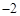 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移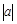 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移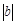 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 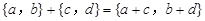 .
.
(1)计算:{3,1}+{1,2};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点O吗? 在图1中画出四边形OABC.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
“鸡兔同笼”是我国古代著名的数学趣题之一.大约在1500年前成书的《孙子算经》中,就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有35个头;从下面数,有94条腿.问笼中各有几只鸡和兔?
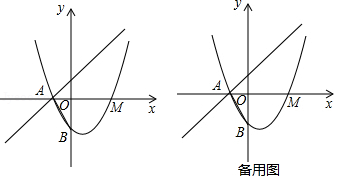
如图所示,顶点为 , 的抛物线 过点 .
(1)求抛物线的解析式;
(2)点 是抛物线与 轴的交点(不与点 重合),点 是抛物线与 轴的交点,点 是直线 上一点(处于 轴下方),点 是反比例函数 图象上一点,若以点 , , , 为顶点的四边形是菱形,求 的值.
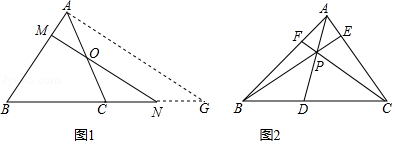
如图1所示,在 中,点 是 上一点,过点 的直线与 , 的延长线分别相交于点 , .
【问题引入】
(1)若点 是 的中点, ,求 的值;
温馨提示:过点 作 的平行线交 的延长线于点 .
【探索研究】
(2)若点 是 上任意一点(不与 , 重合),求证: ;
【拓展应用】
(3)如图2所示,点 是 内任意一点,射线 , , 分别交 , , 于点 , , ,若 , ,求 的值.
如图所示,直线 和圆 相切于点 ,交直径 的延长线于点 .过点 作 的垂线,交 于点 ,交圆 于点 .作平行四边形 ,连接 , , .
(1)求证: ;
(2)求 及 的大小.

某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案.在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
