(本小题满分10分)观察思考
某种在同一平面进行传动的机械装置如图1,图2是它的示意图.其工作原理是:滑块Q在平直滑道l上可以左右滑动,在Q滑动的过程中,连杆PQ也随之运动,并且
PQ带动连杆OP绕固定点O摆动.在摆动过程中,两连杆的接点P在以OP为半径的⊙O上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O作OH ⊥l于点H,并测得
OH = 4分米,PQ = 3分米,OP = 2分米.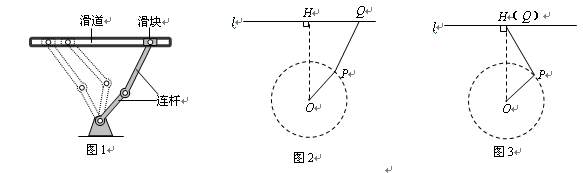
解决问题(1)点Q与点O间的最小距离是 分米;点Q与点O间的最大距离是 分米;点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米.
(2)如图3,小明同学说:“当点Q滑动到点H的位置时,PQ与⊙O是相切的.”你认为他的判断对吗?为什么?
(3)①小丽同学发现:“当点P运动到OH上时,点P到l的距离最小.”事实上,还存在着点P到l距离最大的位置,此时,点P到l的距离是 分米;②当OP绕点O左右摆动时,所扫过的区域为扇形,求这个扇形面积最大时圆心角的度数.
.
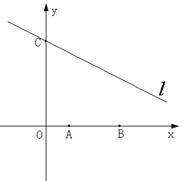
如图,在平面直角坐标系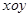 中,点
中,点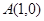 ,点
,点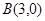 ,点
,点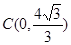 ,直线经过点
,直线经过点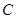 ,
,
(1)若在
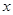 轴上
轴上 方直线
方直线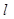 上存在点
上存在点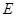 使△
使△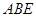 为等边三角形,求直线
为等边三角形,求直线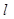 所表达的函数关系式;
所表达的函数关系式;(2)若在
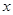 轴上方直线上有且只有
轴上方直线上有且只有 三个点能和
三个点能和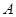 、
、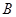 构成直角三角形,求直线
构成直角三角形,求直线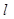 所表达的函数关系式;
所表达的函数关系式;(3)若在
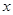 轴上方直线上有且只有一个点在函数
轴上方直线上有且只有一个点在函数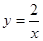 的图形上,求直线
的图形上,求直线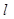 所表达的函数关系式.
所表达的函数关系式.
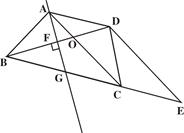
如图,在等腰梯形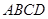 中,
中,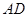 ∥
∥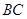 ,AD=AB.过
,AD=AB.过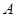 作
作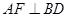 ,交
,交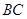 于
于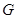 ,延长
,延长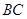 至
至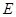 ,使
,使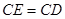 .
.
(1)请指出四边形
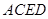 的形状,并证明;
的形状,并证明;(2)如果
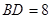 ,
,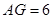 ,求三角形
,求三角形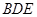 的面积.
的面积.
已知二次函数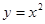
(1)怎样平移这个函数的图象,才能使它经过
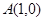 和
和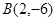 两点?写出平移后的新函数的解析式;
两点?写出平移后的新函数的解析式; (2) 求使新函数的图象位于
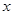 轴上方的实数
轴上方的实数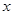 的取值范围。
的取值范围。
已知:△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连结CE,DE。求证:EC=ED.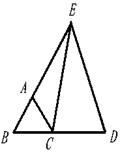
某公司组织340名员工进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆,经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李。(1)请你帮助公司设计三个可行的租车方案;
(2)如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,请你设计租车费用最省的方案?