命题p:关于 的不等式
的不等式 对于一切
对于一切 恒成立,命题q:函数
恒成立,命题q:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围;
某商场预计全年分批购入每台价值为2 000元的电视机共
3 600台.每批都购入x台(x∈N*),且每批均需付运费400元.贮存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43 600元.现在全年只有24 000元资金用于支付这笔费用,请问能否恰当安排每批进货的数量使资金够用?写出你的结论,并说明理由.
已知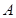 、
、 、
、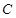 为
为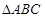 的三内角,且其对边分别为
的三内角,且其对边分别为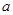 、
、 、
、 ,若
,若 .
.
(Ⅰ)求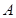 ; (Ⅱ)若
; (Ⅱ)若 ,求
,求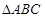 的面积
的面积
 ,若
,若 时有极值,求实数
时有极值,求实数 的值和
的值和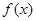 的单调区间;
的单调区间;
若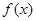 在定义域上是增函数,求实数
在定义域上是增函数,求实数 的取值范围
的取值范围
已知数列
(1)求数列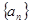 ,
, 的通项公式;
的通项公式;
(2)求数列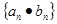 的前
的前 项和
项和 。
。