(本小题14分)如图所示,在四棱锥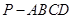 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 底面
底面 ,
, 为
为 的中点.
的中点.
(1)求直线 与
与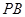 所成角的余弦值;
所成角的余弦值;
(2)在侧面 内找一点
内找一点 ,使
,使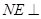 平面
平面 ,并分别求出点
,并分别求出点 到
到 和
和 的距离.
的距离.
设数列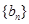 的前
的前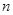 项和为
项和为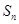 ,且
,且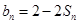 ;数列
;数列 为等差数列,且
为等差数列,且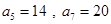 .
.
(1)求数列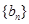 的通项公式;
的通项公式;
(2)若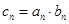 (
(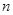 =1,2,3…),
=1,2,3…), 为数列
为数列 的前
的前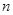 项和.求
项和.求 .
.
已知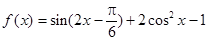
(Ⅰ)求函数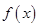 的单调增区间
的单调增区间
(Ⅱ)在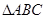 中,
中,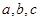 分别是角
分别是角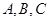 的对边,且
的对边,且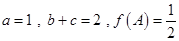 ,求
,求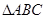 的面积
的面积
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).
| 混合 |
烹调 |
包装 |
|
| A |
1 |
5 |
3 |
| B |
2 |
4 |
1 |
每种糖果的生产过程中,混合的设备至多用机器12 h,烹调的设备最多只能用机器30 h,包装的设备最多只能用机器15 h,每种糖果各生产多少箱可获得最大利润?
已知数列 是等差数列,且
是等差数列,且
(1)求数列 的通项公式;
的通项公式;
(2)(文)令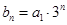 ,求
,求 的前n项和.
的前n项和.
(2)(理)令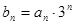 ,求
,求 的前n项和.
的前n项和.
在 中,
中,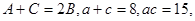 求
求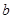 的值。
的值。