(本小题满分12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对楼市“楼市限购令”赞成人数如下表.
| 月收入(单位百元) |
[15,25 |
[25,35 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| |
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
| 赞成 |
 |
 |
|
| 不赞成 |
 |
 |
|
| 合计 |
|
|
|
(Ⅱ)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为  ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
(本题满分12分)已知
(1)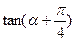 的值;
的值;
(2)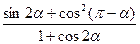 的值.
的值.
(本小题满分10分)
某校有学生会干部7名,其中男干部有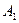 ,A
,A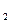 ,A
,A ,A
,A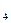 共4人;女干部有B
共4人;女干部有B ,B
,B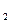 ,B
,B 共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
共3人.从中选出男、女干部各1名,组成一个小组参加某项活动.
(Ⅰ)求A 被选中的概率;
被选中的概率;
(Ⅱ)求A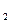 ,B
,B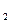 不全被选中的概率.
不全被选中的概率.
(本小题满分10分)
已知 =1,
=1,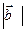 =
=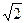 .
.
(Ⅰ)若 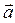 与
与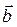 的夹角为
的夹角为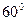 ,求
,求 ;
;
(Ⅱ)若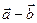 与
与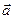 垂直,求
垂直,求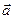 与
与 的夹角.
的夹角.
(本小题满分14分)
已知圆C经过点 ,圆心落在
,圆心落在 轴上(圆心与坐标原点不重合),且与直线
轴上(圆心与坐标原点不重合),且与直线 相切.
相切.
(Ⅰ)求圆C的标准方程;
(Ⅱ)求直线Y="X" 被圆C所截得的弦长;
(Ⅲ)l2是与l1垂直并且在Y轴上的截距为b的直线,若)l2与圆C有两个不同的交点,求b的取值范围.
(本小题满分12分)
某学校举办消防知识竞赛,总共 7 个题中,分值为 10 分的有 共4 个,分值为 20 分的有
共4 个,分值为 20 分的有 共3个,每位选手都要分别从 4 个 10 分题和 3 个 20 分题中各随机抽取 1 题参赛.已知甲选手 4 个 10 分题中只有
共3个,每位选手都要分别从 4 个 10 分题和 3 个 20 分题中各随机抽取 1 题参赛.已知甲选手 4 个 10 分题中只有 不会,3个 20分题中只会
不会,3个 20分题中只会 .
.
(Ⅰ)求甲选手恰好得30分的概率;
(Ⅱ)求甲选手得分超过10分的概率.