(本小题满分14分)
已知圆C经过点 ,圆心落在
,圆心落在 轴上(圆心与坐标原点不重合),且与直线
轴上(圆心与坐标原点不重合),且与直线 相切.
相切.
(Ⅰ)求圆C的标准方程;
(Ⅱ)求直线Y="X" 被圆C所截得的弦长;
(Ⅲ)l2是与l1垂直并且在Y轴上的截距为b的直线,若)l2与圆C有两个不同的交点,求b的取值范围.
(本小题满分12分)
已知函数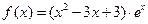 ,其定义域为
,其定义域为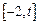 (
(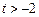 ),设
),设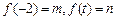 .
.
(Ⅰ)试确定 的取值范围,使得函数
的取值范围,使得函数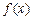 在
在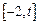 上为单调函数;
上为单调函数;
(Ⅱ)试判断 的大小并说明理由;
的大小并说明理由;
(Ⅲ)求证:对于任意的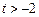 ,总存在
,总存在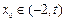 ,满足
,满足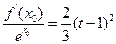 ,并确定这样的
,并确定这样的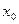 的个数.
的个数.
(本小题10分)
已知抛物线 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。
(I)若m=1,且直线 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(II)问是否存在定点M,不论直线 绕点M如何转动,使得
绕点M如何转动,使得 恒为定值。
恒为定值。
(本小题9分)
如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。
(本小题8分)
数列 满足
满足
 ,先计算前4项后,猜想
,先计算前4项后,猜想 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
已知函数 有下列性质:“若
有下列性质:“若 ,则存在
,则存在 ,使得
,使得 ”成立
”成立
(I)证明:若 ,则唯一存在
,则唯一存在 ,使得
,使得 ;
;
(II) 设A、B、C是函数 图象上三个不同的点,试判断△ABC的形状,并说明理由
图象上三个不同的点,试判断△ABC的形状,并说明理由