(本小题满分12分)已知a∈(0,6),b∈(0,6)
(I)求∣a-b∣≤1的概率;
(Ⅱ)以a,b作为直角三角形两直角边的边长,则斜边长小于6的概率.
如图,点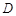 为锐角
为锐角 的内切圆圆心,过点
的内切圆圆心,过点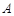 作直线
作直线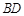 的垂线,垂足为
的垂线,垂足为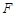 ,圆
,圆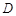 与边
与边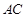 相切于点
相切于点 .若
.若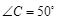 ,求
,求 的度数.
的度数.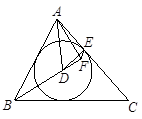
已知数列 满足
满足 ,
,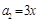 ,
,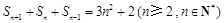 ,
,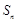 是数列
是数列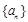 的前
的前 项和.
项和.
(1)若数列 为等差数列.
为等差数列.
(ⅰ)求数列的通项 ;
;
(ⅱ)若数列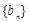 满足
满足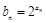 ,数列
,数列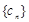 满足
满足 ,试比较数列
,试比较数列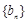 前
前 项和
项和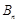 与
与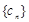 前
前 项和
项和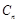 的大小;
的大小;
(2)若对任意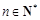 ,
,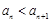 恒成立,求实数
恒成立,求实数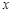 的取值范围.
的取值范围.
已知函数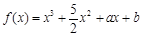 (
(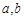 为常数),其图象是曲线
为常数),其图象是曲线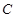 .
.
(1)当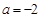 时,求函数
时,求函数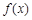 的单调减区间;
的单调减区间;
(2)设函数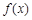 的导函数为
的导函数为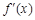 ,若存在唯一的实数
,若存在唯一的实数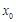 ,使得
,使得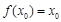 与
与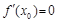 同时成立,求实数
同时成立,求实数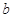 的取值范围;
的取值范围;
(3)已知点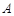 为曲线
为曲线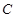 上的动点,在点
上的动点,在点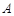 处作曲线
处作曲线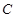 的切线
的切线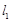 与曲线
与曲线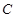 交于另一点
交于另一点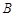 ,在点
,在点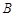 处作曲线
处作曲线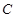 的切线
的切线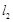 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数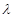 ,使得
,使得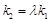 ?若存在,求出
?若存在,求出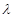 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知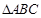 的三个顶点
的三个顶点 ,
,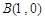 ,
,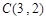 ,其外接圆为
,其外接圆为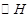 .
.
(1)若直线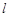 过点
过点 ,且被
,且被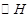 截得的弦长为2,求直线
截得的弦长为2,求直线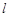 的方程;
的方程;
(2)对于线段 上的任意一点
上的任意一点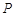 ,若在以
,若在以 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点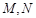 ,使得点
,使得点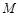 是线段
是线段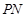 的中点,求
的中点,求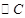 的半径
的半径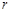 的取值范围.
的取值范围.
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点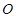 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点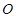 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为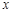 米,圆心角为
米,圆心角为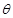 (弧度).
(弧度).
(1)求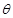 关于
关于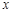 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为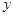 ,求
,求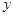 关于
关于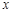 的函数关系式,并求出
的函数关系式,并求出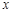 为何值时,
为何值时,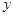 取得最大值?
取得最大值?