某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点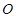 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点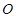 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为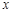 米,圆心角为
米,圆心角为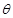 (弧度).
(弧度).
(1)求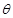 关于
关于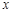 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为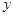 ,求
,求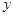 关于
关于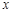 的函数关系式,并求出
的函数关系式,并求出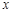 为何值时,
为何值时,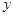 取得最大值?
取得最大值?
.选修 4-1:几何证明选讲
4-1:几何证明选讲
如图,直线 经过⊙
经过⊙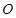 上的点
上的点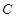 ,并且
,并且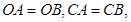 ⊙
⊙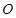 交直
交直 线
线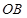 于
于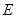 ,
,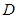 ,连接
,连接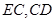 .
.
(I)求证:直线 是⊙
是⊙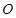 的切线;
的切线;
(II)若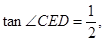 ⊙
⊙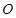 的半径为
的半径为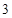 ,求
,求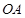 的长.
的长.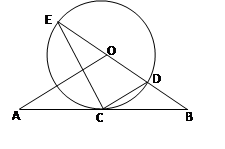
(本小题满分12分)
已知函数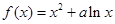
(Ⅰ)当a=﹣2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)=  +
+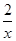 在
在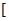 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.
(本小题满分12分)
已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为 和
和 ,且|
,且|
 |=2,
|=2,
点(1, )在该椭圆上.
)在该椭圆上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过 的直线
的直线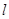 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A B的面积为
B的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线
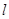 相切是圆的方程.
相切是圆的方程.
(本小题满分12分)
我校高三年级进行了一次水平测试.用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计成绩的分组及各组的频数如下:
[40,50), 2; [50,60), 3; [60,70), 10; [70,80), 15; [80,90), 12; [90,100], 8.
(Ⅰ)完成样本的频率分布表;画出频率分布直方图.
(Ⅱ)估计成绩在85分以下的学生比例;
(Ⅲ)请你根据以上信息去估计样本的众数、中位数、平均数.(精确到0.01)
.(本小题满分12分)
如图,四棱锥P—ABCD中,底面ABCD是边长为 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=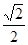 AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.