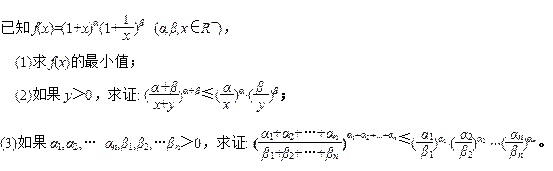
(1)解不等式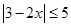 ;
;
(2)已知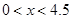 ,求
,求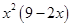 的最大值.
的最大值.
(选修4-5:不等式选讲)设函数 .
.
(1)解不等式 ;
;
(2)若对任意实数 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
(选修4-4:坐标系与参数方程)
在直角坐标系 中,圆
中,圆 的方程为
的方程为 .以
.以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)射线
 与圆
与圆 的交点为
的交点为 、
、 两点,求
两点,求 点的极坐标.
点的极坐标.
已知函数 (
( ).
).
(1)当 时,求
时,求 在
在 的最小值;
的最小值;
(2)若 存在单调递减区间,求
存在单调递减区间,求 的取值范围.
的取值范围.
某鱼类养殖户在一个鱼池中养殖一种鱼,每季养殖成本为 元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
鱼池产量( ) ) |
 |
 |
鱼的市场价格(元/ ) ) |
 |
 |
|
| 概率 |
 |
 |
概率 |
 |
 |
(1)设 表示在这个鱼池养殖
表示在这个鱼池养殖 季这种鱼的利润,求
季这种鱼的利润,求 的分布列和期望;
的分布列和期望;
(2)若在这个鱼池中连续 季养殖这种鱼,求这
季养殖这种鱼,求这 季中至少有
季中至少有 季的利润不少于
季的利润不少于 元的概率.
元的概率.