某鱼类养殖户在一个鱼池中养殖一种鱼,每季养殖成本为 元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
鱼池产量( ) ) |
 |
 |
|
鱼的市场价格(元/ ) ) |
 |
 |
| 概率 |
 |
 |
|
概率 |
 |
 |
(1)设 表示在这个鱼池养殖
表示在这个鱼池养殖 季这种鱼的利润,求
季这种鱼的利润,求 的分布列和期望;
的分布列和期望;
(2)若在这个鱼池中连续 季养殖这种鱼,求这
季养殖这种鱼,求这 季中至少有
季中至少有 季的利润不少于
季的利润不少于 元的概率.
元的概率.
已知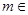 R,函数
R,函数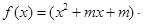 e
e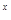 .
.
(1)若函数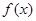 没有零点,求实数
没有零点,求实数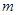 的取值范围;
的取值范围;
(2)若函数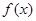 存在极大值,并记为
存在极大值,并记为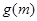 ,求
,求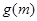 的表达式;
的表达式;
(3)当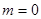 时,求证:
时,求证: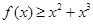 .
.
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数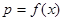 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
已知向量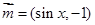 ,向量
,向量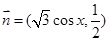 ,函数
,函数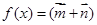 ·
·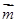 .
.
(1)求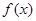 的最小正周期T;
的最小正周期T;
(2)若方程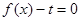 在
在 上有解,求实数
上有解,求实数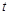 的取值范围.
的取值范围.
已知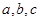 是
是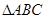 中
中 的对边,
的对边,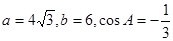 .
.
(1)求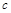 ;
;
(2)求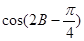 的值.
的值.
已知函数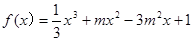 ,
,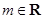 .
.
(Ⅰ)当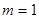 时,求曲线
时,求曲线 在点
在点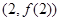 处的切线方程;
处的切线方程;
(Ⅱ)若 在区间
在区间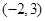 上是减函数,求
上是减函数,求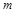 的取值范围.
的取值范围.