已知箱子里装有3个白球、3个黑球,这些球除颜色外完全相同,每次游戏从箱子里取出2个球,若这两个球的颜色相同,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中获奖的概率;
(Ⅱ)求在3次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望
已知等差数列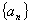 ,
,
(1)求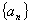 的通项公式;
的通项公式;
(2)令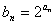 ,求数列
,求数列 的前
的前 项和
项和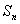 ;
;
在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率。
如图,已知棱柱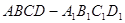 的底面是菱形,且面
的底面是菱形,且面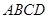 ,
,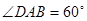 ,
,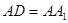 ,
,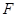 为棱
为棱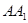 的中点,
的中点,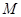 为线段
为线段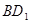 的中点,
的中点,
(1)求证: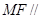 面
面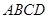 ;
;
(2)求证: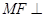 面
面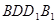
已知函数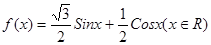
(1)求函数的最小正周期 (2)求函数的单调递增区间 (3)求函数的最大值,并求出对应的X值的取值集合。
已知点A(1,-1),B(5,1),直线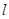 经过点A,且斜率为
经过点A,且斜率为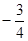 ,
,
(1)求直线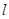 的方程。(2)求以B为圆心,并且与直线
的方程。(2)求以B为圆心,并且与直线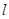 相切的圆的标准方程。
相切的圆的标准方程。