已知椭圆 的一个焦点
的一个焦点 与抛物线
与抛物线 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为
,倾斜角为 的直线
的直线 过点
过点 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为 ,问抛物线
,问抛物线 上是否存在一点
上是否存在一点 ,使得
,使得 与
与 关于直线
关于直线 对称,若存在,求出点
对称,若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知函数 .
.
(1)当 时,如果函数
时,如果函数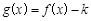 仅有一个零点,求实数
仅有一个零点,求实数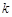 的取值范围;
的取值范围;
(2)当 时,试比较
时,试比较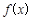 与1的大小;
与1的大小;
(3)求证:
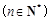
已知 ,数列
,数列 是首项为
是首项为 ,公比也为
,公比也为 的等比数列,令
的等比数列,令
(Ⅰ)求数列 的前
的前 项和
项和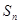 ;
;
(Ⅱ)当数列 中的每一项总小于它后面的项时,求
中的每一项总小于它后面的项时,求 的取值范围.
的取值范围.
已知向量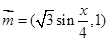 ,
,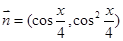 ,
,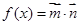
(Ⅰ)若 ,求
,求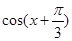 的值;
的值;
(Ⅱ)在 中,角
中,角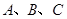 的对边分别是
的对边分别是 ,且满足
,且满足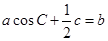 ,求函数
,求函数 的取值范围.
的取值范围.
关于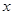 的不等式
的不等式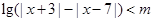 .
.
(Ⅰ)当 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数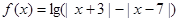 ,当
,当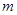 为何值时,
为何值时,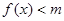 恒成立?
恒成立?
在平面直角坐标系xoy中,曲线C1的参数方程为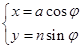 (
(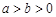 ,
,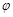 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,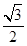 )对应的参数j=
)对应的参数j=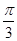 ,曲线C2过点D(1,
,曲线C2过点D(1,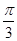 ).
).
(I)求曲线C1,C2的直角坐标方程;
(II)若点A(r1,q),B(r2,q+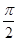 )在曲线C1上,求
)在曲线C1上,求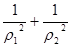 的值.
的值.