某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
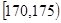 |
30 |
② |
| 第4组 |
 |
20 |
0.200 |
| 第5组 |
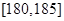 |
10 |
0.100 |
| 合计 |
100 |
1.00 |

(本小题满分12分)
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" =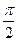 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(I)当x=2时,求证:BD⊥EG ;
(II)若以F、B、C、D为顶点的三棱锥的体积记为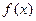 ,
,
求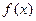 的最大值;
的最大值;
(III)当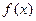 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.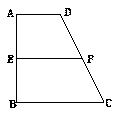
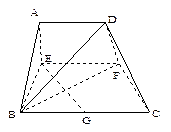 ]
]
(本小题满分12分)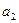 ,
,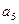 是方程
是方程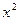
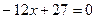 的两根, 数列
的两根, 数列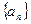 是公差为正的等差数列,数列
是公差为正的等差数列,数列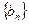 的前
的前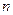 项和为
项和为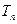 ,且
,且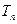
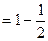
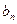
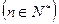 .
.
(I)求数列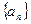 ,
,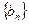 的通项公式; (II)记
的通项公式; (II)记 =
=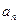
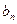 ,求数列
,求数列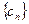 的前
的前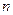 项和
项和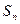 .
.
本小题满分12分)
已知关于x的二次函数f(x)=ax2-4bx+1.
(I)已知集合P={-1,1,2,3,4,5},Q={-2,-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(II)在区域内随机任取一点(a,b).求函数 y=f(x)在区间[1,+∞)上是增函数的概率.
y=f(x)在区间[1,+∞)上是增函数的概率.
(本小题 满分10分)
满分10分)
已知向量
 ,定义
,定义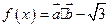
(I)求函数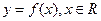 的单调递减区间;
的单调递减区间;
(II)若函数 为偶函数,求
为偶函数,求 的值。
的值。
(本小题满分10分)
在某学校组织的一次蓝球定点投蓝训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投三次。某同学在 A处的命中率
A处的命中率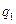 为0.25,在B处的命中率为
为0.25,在B处的命中率为 .该同学选择
.该同学选择 先在A处投一球,以后都在B处投,用
先在A处投一球,以后都在B处投,用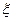 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为 
 |
0 |
2 |
3 |
4 |
5 |
 |
0.03 |
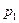 |
 |
 |
 |
 求
求 的值;
的值; 求随机变量
求随机变量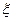 的数学期量
的数学期量 ;
; 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超
试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超 过3分的概率的大小。
过3分的概率的大小。